Question 17 (15 Marks):
(a) Diagram 7.1 shows the shape of the cake that Cikgu Alam wants to order to celebrate her class’s cheerful victory. The two-tiered cake consists of a combination of a cuboid and a cylinder with a radius of 14 cm.
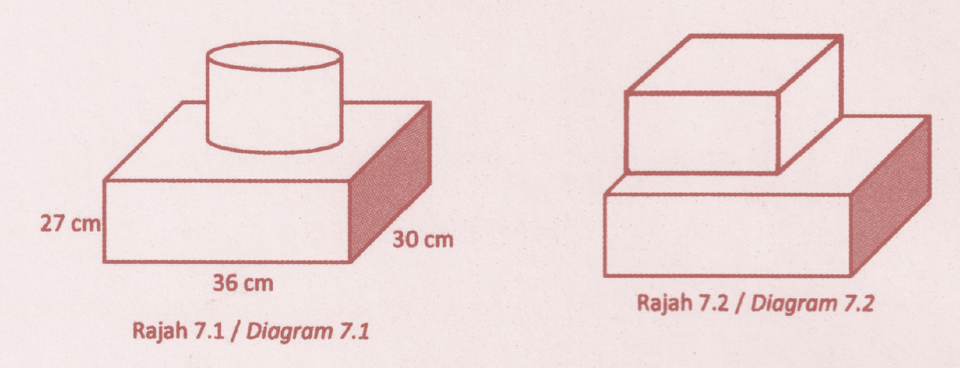
The total volume of the cake in Figure 7.1 is 34 998 cm3. Cikgu Alam then wants to change the cylindrical cake to a cube-shaped cake as in Figure 7.2 without changing the original volume of the cake.
[use π = 22/7 ]
(i) Calculate the height, in cm, of the cylindrical cake in Figure 7.1. Round the correct answer to 3 significant figures. [4 marks]
(ii) Calculate the length, in cm, of the sides of the cube -shaped cake. Round off the correct answer to 2 significant figures. [3 marks]
Solution:
(a)(i)
(a)(ii)
(a) Diagram 7.1 shows the shape of the cake that Cikgu Alam wants to order to celebrate her class’s cheerful victory. The two-tiered cake consists of a combination of a cuboid and a cylinder with a radius of 14 cm.

The total volume of the cake in Figure 7.1 is 34 998 cm3. Cikgu Alam then wants to change the cylindrical cake to a cube-shaped cake as in Figure 7.2 without changing the original volume of the cake.
[use π = 22/7 ]
(i) Calculate the height, in cm, of the cylindrical cake in Figure 7.1. Round the correct answer to 3 significant figures. [4 marks]
(ii) Calculate the length, in cm, of the sides of the cube -shaped cake. Round off the correct answer to 2 significant figures. [3 marks]
Solution:
(a)(i)
(a)(ii)
(b):
Cikgu Alam decides to order a cake as shown in Figure 7.2. During the ceremony, Cikgu Alam cut the first part of the cube -shaped cake. The remainder of the cake after the first cut is shown in Figure 7.3.
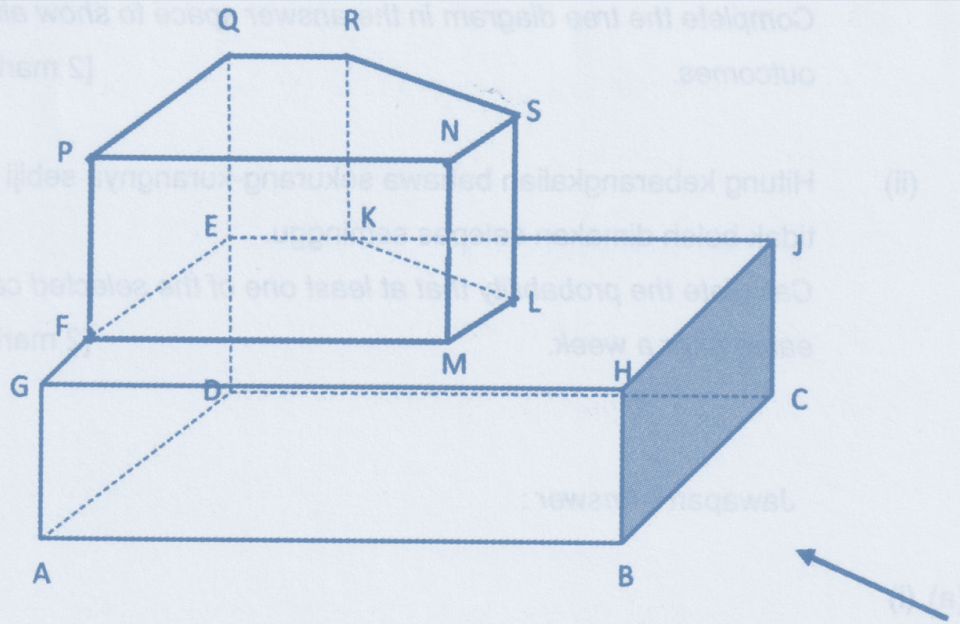 Diagram 7.3
Diagram 7.3
The edges of RK and SL are perpendicular. Given GF = ML = 12 cm. By using a scale of 1 : 3, draw the elevation of the remaining cake on a vertical plane parallel to BC, as viewed from Y. [4 marks]
Solution:
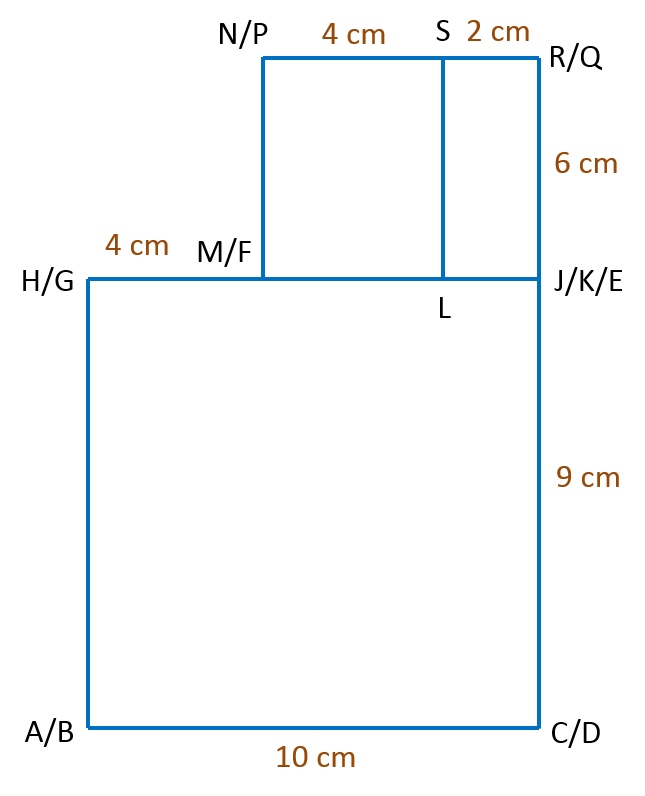
Cikgu Alam decides to order a cake as shown in Figure 7.2. During the ceremony, Cikgu Alam cut the first part of the cube -shaped cake. The remainder of the cake after the first cut is shown in Figure 7.3.
 Diagram 7.3
Diagram 7.3The edges of RK and SL are perpendicular. Given GF = ML = 12 cm. By using a scale of 1 : 3, draw the elevation of the remaining cake on a vertical plane parallel to BC, as viewed from Y. [4 marks]
Solution:

(c):
The probability that the ordered cake cannot be eaten after a week is 1/8. Two cakes are chosen at random.
(i) Complete the tree diagram in the answer space to show all possible outcomes. [2 marks]
(ii) Calculate the probability that at least one of the selected cakes cannot be eaten after a week. [2 marks]
Answer:

Solution:
(c)(i)

(c)(ii)
The probability that the ordered cake cannot be eaten after a week is 1/8. Two cakes are chosen at random.
(i) Complete the tree diagram in the answer space to show all possible outcomes. [2 marks]
(ii) Calculate the probability that at least one of the selected cakes cannot be eaten after a week. [2 marks]
Answer:

Solution:
(c)(i)

(c)(ii)