SPM Mathematics Trial 2021 (Selangor), Paper 2 (Question 1 & 2)

Question 1:
Solve the following equation:
3x (3 – x) = -(4 + 2x)
(4 marks)

Solution:
3x (3 – x) = -(4 + 2x)
9x – 3x² = -4 – 2x
3x² – 9x – 2x – 4 = 0
3x² – 11x – 4 = 0
(x – 4)(3x + 1) = 0
x = 4, x = –1/3

Question 2:
Diagram 1 shows a prism-shaped solid with a rectangular base ABCD lying on the horizontal plane. The surface ABGF is the uniform cross-section of the prism. ADEF is a square.


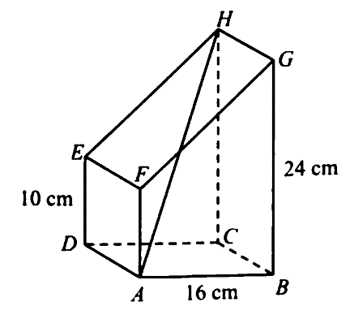
Calculate the angle between the plane ABCD and the line AH.
[4 marks]


Solution:

$\begin{array}{l}\text{By using Pythagores’ theorem}\\ A{C}^2=A{B}^2+B{C}^2\\ AC=\sqrt{A{B}^2+B{C}^2}\\ =\sqrt{{16}^2+{10}^2}\\ =\sqrt{356}\text{ cm}\\ \\ \text{Angle between the plane }ABCD\text{ and the line }AH\\ =\angle HAC\\ \tan \angle HAC=\frac{HC}{AC}\\ =\frac{24}{\sqrt{356}}\\ \angle HAC={\tan }^{-1}\frac{24}{\sqrt{356}}\\ ={51.83}^o\end{array}$