SPM Mathematics Trial 2021 (Selangor), Paper 2 (Question 3 & 4)

Question 3:
(a) Diana uses 1.26 m of red ribbon to stick around a circular shaped cardboard. Calculate the radius, in m, of the cardboard.
( Use π = 3.142)
(4 marks)

(b) Diana noticed that the site of a recreational park built near her house is round in shape and has a centre, O. There is a square shaped line measuring 30 m of length painted on the recreation area as shown in Diagram 2. The shaded area in Diagram 2 is tiled. Radius of the smaller circle is 11 m.


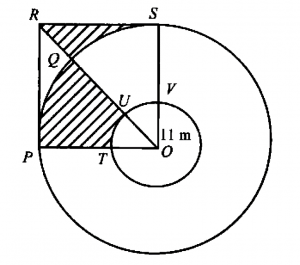
Calculate the tiled area. (Use π=3.142 )
State your answer correct to two decimal places.
(3 marks)


Solution:
(a)

$\begin{array}{l}2\pi r=1.23\\ r=\frac{1.26}{2\pi }\\ r=\frac{1.26}{2\left(3.142\right)}\\ r=0.2\text{ m}\end{array}$


(b)

$\begin{array}{l}\text{radius }OP,r_1=30\text{ m}\\ \text{radius }OT,r_2=11\text{ m}\\ \angle POQ=\frac{{90}^o}{2}={45}^o\\ \\ \text{Shaded region }PTUQ\\ =\pi {\left(r_1\right)}^2-\pi {\left(r_2\right)}^2\\ =\frac{45}{360}\times 3.142\times \left({30}^2-{11}^2\right)\\ =305.953{\text{ m}}^2\\ \\ \text{Shaded region }QRS\\ =\text{ Area of triangle }ORS-\text{Area of sector }OSQ\\ =\left(\frac{1}{2}\times 30\times 30\right)-\left(\frac{45}{360}\times 3.142\times {30}^2\right)\\ =450-353.475\\ =96.525{\text{ m}}^2\\ \\ \text{Thus, the tiled area}\\ =305.953+96.525\\ =402.48{\text{ m}}^2\end{array}$

Soalan 4:
(a) Complete the following statements by using a proper quantifier to form a true statement.
(i)  ………………….. state flags in Malaysia has red colour.
(ii) ………………….. polygons have equal number of axis as the number of sides.
[2 marks]

(b) Write down Premise 2 to complete the following argument:
Premise 1 : If n is a perfect square, then square root of n is an integer.
Premise 2 : ……………………………………………………………………………..
Conclusion : Square root of 81 is an integer.
[1 mark]

(c) Write down the converse of the following implication.

If △PQR is an equilateral triangle, then the value of each interior angle is 60∘.

[1 mark]

Penyelesaian:
(a)(i)  Some  state flags in Malaysia has red colour.

(a)(ii) Some  polygons have equal number of axis as the number of sides.

(b) Premise 2 : 81 is a perfect square.

(c) Converse of the implication : If the value of each interior angle is 60^∘, then △ PQR is an equilateral triangle.