SPM Mathematics Trial 2021 (Kelantan), Paper 2 (Question 16)

Question 16 (15 Marks):
Diagram 6 shows the position of the swimming pool, fish pond and house of Mrs. Halina and her two children, Hazeq and Haqq. The built-up swimming pool is equidistable between the three houses of Mrs. Halina, Haqq and Hazeq.

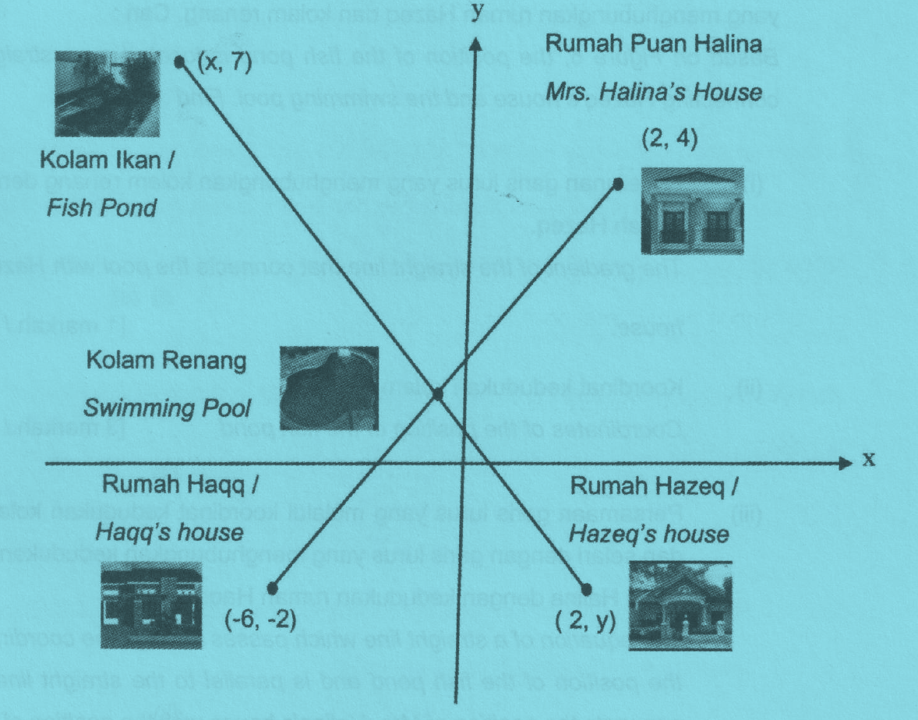Diagram 6

(a) Based on the Diagram 6 above,
(i) find the coordinates of the position of the pool. [2 marks]
(ii) calculate the distance between Haqq’s house and the pool? [2 marks]
(iii) Find the coordinates of Hazeq’s house position. [4 marks]


Solution:
(a)(i)

$\begin{array}{l}\text{Coordinates of the position of the pool}\\ \text{= Midpoint of Haqq’s and Mrs. Halina’s house}\\ =\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)\\ =\left(\frac{-6+2}{2},\frac{-2+4}{2}\right)\\ =\left(-2,1\right)\end{array}$


(a)(ii)

$\begin{array}{l}\text{Distance between Haqq’s house and the pool}\\ =\sqrt{{\left(x_1-x_2\right)}^2-{\left(y_1-y_2\right)}^2}\\ =\sqrt{{\left(-6-\left(-2\right)\right)}^2+{\left(-2-1\right)}^2}\\ =\sqrt{{\left(-4\right)}^2+{\left(-3\right)}^2}\\ =\sqrt{25}\\ =5\text{ units}\end{array}$


(a)(iii)

$\begin{array}{l}\text{Distance between Hazeq’s house and the pool}=5\text{ units}\\ \sqrt{{\left(2-\left(-2\right)\right)}^2+{\left(y-1\right)}^2}=5\\ 4^2+{\left(y-1\right)}^2=5^2\\ 16+y^2-2y+1=25\\ 16+y^2-2y+1-25=0\\ y^2-2y-8=0\\ \left(y+2\right)\left(y-4\right)=0\\ y=-2\text{ or }y=4(\text{rejected)}\\ \\ \text{Thus, the coordinates of Hazeq’s house}=\left(2,-2\right).\end{array}$

(b):
Based on Figure 6, the position of the fish pond is located on a straight line connecting Hazeq’s house and the swimming pool. Find:

(i) The gradient of the straight line that connects the pool with Hazeq’s house. [1 mark]

(ii) Coordinates of the position of the fish pond. [3 marks]

(iii) The equation of a straight line which passes through the coordinates of the position of the fish pond and is parallel to the straight line which connects the position of Mrs. Halina’s house with the position of Haqq’s house. [3 marks]


Solution:
(b)(i)

$\begin{array}{l}\text{Gradient of the straight line}\\ =\frac{y_2-y_1}{x_2-x_1}\\ =\frac{-2-1}{2-\left(-2\right)}\\ =-\frac{3}{4}\end{array}$


(b)(ii)

$\begin{array}{l}\text{The gradient of the straight line that connects the swimming pool and the}\\ \text{fish pond}=-\frac{3}{4}\\ \frac{1-7}{-2-x}=-\frac{3}{4}\\ -6\left(4\right)=-3\left(-2-x\right)\\ -24=6+3x\\ 3x=-30\\ x=-10\\ \\ \text{Thus, the coordinates of the position of the fish pond}=\left(-10,7\right).\end{array}$


(b)(iii)

$\begin{array}{l}\text{Gradient of the straight line of Mrs. Halina and Haqq’s house}\\ =\frac{4-\left(-2\right)}{2-\left(-6\right)}\\ =\frac{6}{8}=\frac{3}{4}\\ \\ \text{y-intercept of the parallel line that passed through point }\left(-10,7\right),\\ y_1=m{x}_1+c\\ 7=\frac{3}{4}\left(-10\right)+c\\ 7=\frac{-30}{4}+c\\ c=7+\frac{30}{4}\\ c=\frac{29}{2}\\ \\ \text{Thus, the equation of straight line }y=mx+c\text{ is }y=\frac{3}{4}x+\frac{29}{2}.\end{array}$