Question 1:
The time taken, t in hour, to mow a lawn varies directly as the area of a field, L in m2, and inversely as the number of workers, w. Given that 5 workers need 3 hours to mow the grasses of the field with area of 4 × 104 m2.
(a) Find the equation that relate t in terms of L and w. [2 marks]
(b) Calculate the minimum number of workers needed to mow the grass of a field with area of 1.6 × 105 m2 within 8 hours. [2 marks]
Solution:
(a)
$$ \begin{aligned} & t \propto L \\ & t \propto \frac{1}{w} \\ & t \propto \frac{L}{w} \\ & t=\frac{k L}{w} \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} & \text { Given that } w=5, t=3, L=4 \times 10^4 \\ & \begin{aligned} 3 & =\frac{k\left(4 \times 10^4\right)}{5} \\ k & =\frac{15}{4 \times 10^4} \\ & =\frac{3}{8000} \end{aligned} \end{aligned}\\ &\text { Thus, } t=\frac{3 L}{8000 w} \end{aligned} $$
$$ \begin{aligned} & \text { When } t=8, L=1.6 \times 10^5 \\ & 8=\frac{3\left(1.6 \times 10^5\right)}{8000 w} \\ & w=\frac{3\left(1.6 \times 10^5\right)}{8000 \times 8} \\ & =7.5 \\ & =8 \text { workers (minimum) } \end{aligned} $$
The time taken, t in hour, to mow a lawn varies directly as the area of a field, L in m2, and inversely as the number of workers, w. Given that 5 workers need 3 hours to mow the grasses of the field with area of 4 × 104 m2.
(a) Find the equation that relate t in terms of L and w. [2 marks]
(b) Calculate the minimum number of workers needed to mow the grass of a field with area of 1.6 × 105 m2 within 8 hours. [2 marks]
Solution:
(a)
$$ \begin{aligned} & t \propto L \\ & t \propto \frac{1}{w} \\ & t \propto \frac{L}{w} \\ & t=\frac{k L}{w} \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} & \text { Given that } w=5, t=3, L=4 \times 10^4 \\ & \begin{aligned} 3 & =\frac{k\left(4 \times 10^4\right)}{5} \\ k & =\frac{15}{4 \times 10^4} \\ & =\frac{3}{8000} \end{aligned} \end{aligned}\\ &\text { Thus, } t=\frac{3 L}{8000 w} \end{aligned} $$
$$ \begin{aligned} & \text { When } t=8, L=1.6 \times 10^5 \\ & 8=\frac{3\left(1.6 \times 10^5\right)}{8000 w} \\ & w=\frac{3\left(1.6 \times 10^5\right)}{8000 \times 8} \\ & =7.5 \\ & =8 \text { workers (minimum) } \end{aligned} $$
Question 2:
Diagram 1 in the answer space shows a square PQRS drawn on a square grid with sides of 1 unit. Y is a point that move inside the square.
(a) On Diagram 1, draw the locus of point Y which always moves 3 units from point K. [1 mark]
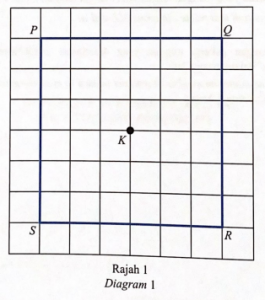
(b) Calculate the distance travelled by locus Y in 2(a). [2 marks]
Solution:
(a)
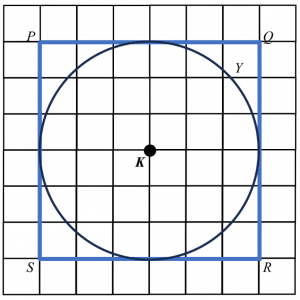
(b)
$$ \begin{aligned} &\text { Distance travelled by locus } Y \text { (Circumference of circle) }\\ &\begin{aligned} & =2 \times \pi \times r \\ & =2 \times \frac{22}{7} \times 3 \\ & =\frac{132}{7}=18 \frac{6}{7} \mathrm{units} \end{aligned} \end{aligned} $$
Diagram 1 in the answer space shows a square PQRS drawn on a square grid with sides of 1 unit. Y is a point that move inside the square.
(a) On Diagram 1, draw the locus of point Y which always moves 3 units from point K. [1 mark]

(b) Calculate the distance travelled by locus Y in 2(a). [2 marks]
Solution:
(a)

(b)
$$ \begin{aligned} &\text { Distance travelled by locus } Y \text { (Circumference of circle) }\\ &\begin{aligned} & =2 \times \pi \times r \\ & =2 \times \frac{22}{7} \times 3 \\ & =\frac{132}{7}=18 \frac{6}{7} \mathrm{units} \end{aligned} \end{aligned} $$