Question 3:
Malware Internet company has 5 Internet channels labelled P, Q, R and S to send messages.

Draw a graph with multiple edges and loops based on the given information. Hence, determine the sum of degrees.
[3 marks]
Solution:
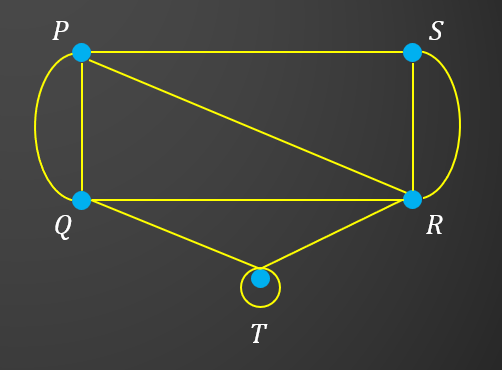
$$ \begin{aligned} \text { Sum of degrees } & =2 \times \text { Number of edges } \\ & =2 \times 10 \\ & =20 \end{aligned} $$
Malware Internet company has 5 Internet channels labelled P, Q, R and S to send messages.
Table 1 shows the number of messages that can be sent by each channel.

Draw a graph with multiple edges and loops based on the given information. Hence, determine the sum of degrees.
[3 marks]
Solution:


$$ \begin{aligned} \text { Sum of degrees } & =2 \times \text { Number of edges } \\ & =2 \times 10 \\ & =20 \end{aligned} $$
Question 4:
(a) State the antecedent and consequent for the following statement. [2 marks]
If x is a multiple of 6 , then x is a multiple of 3.
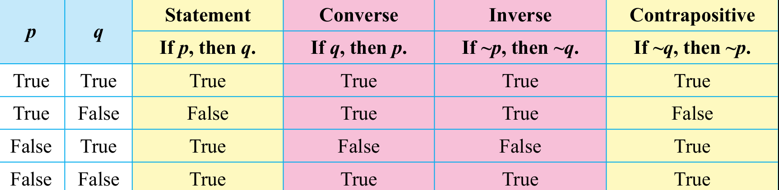
(b) Write the converse for the following implication. Hence, determine whether the converse is true or false.
[2 marks]
$$ \text { If } x=30^{\circ} \text {, then } \sin x=0.5 $$
Solution:
Implication “If p , then q “
A statement “if p, then q” is known as an implication where
– p is denoted as the antecedent.
– q is denoted as the consequent.
(a)
Antecedent : x is multiple of 6
Consequent: x is multiple of 3
(b)
$$ \text { Converse } \sim \text { If } \sin x=0.5, \text { then } x=30^{\circ} $$
$$ \text { False, because if } \sin x=0.5, x \text { consists of two values (1st and 2nd quadrant), } $$
$$ x=30^{\circ} \text { or } x=\left(180^{\circ}-30^{\circ}\right)=150^{\circ} $$
(a) State the antecedent and consequent for the following statement. [2 marks]
If x is a multiple of 6 , then x is a multiple of 3.
(b) Write the converse for the following implication. Hence, determine whether the converse is true or false.
[2 marks]
$$ \text { If } x=30^{\circ} \text {, then } \sin x=0.5 $$
Solution:
Implication “If p , then q “
A statement “if p, then q” is known as an implication where
– p is denoted as the antecedent.
– q is denoted as the consequent.
(a)
Antecedent : x is multiple of 6
Consequent: x is multiple of 3
(b)

$$ \text { Converse } \sim \text { If } \sin x=0.5, \text { then } x=30^{\circ} $$
$$ \text { False, because if } \sin x=0.5, x \text { consists of two values (1st and 2nd quadrant), } $$
$$ x=30^{\circ} \text { or } x=\left(180^{\circ}-30^{\circ}\right)=150^{\circ} $$