(a) Given the cos θ∘ = -0.5150 and 90∘ ≤ θ ≤ 270∘, calculate the value of θ. [2 marks]
(b)(i) On diagram 2 in the answer space, sketch the graph y = 1.5 cos 2x – 1 with the condition 0∘ ≤ θ ≤ 360∘. [2 marks]
(b)(ii) Based on the graph that has been drawn, state the effect of changing the graph when given an amplitude value of 3 . [1 mark]
Solution:
(a)
cos θ∘ = -0.5150 ⇐ Negative value. θ is in quadrant II or III.
Corresponding reference angle,
α = cos-1 0.5150
= 59∘
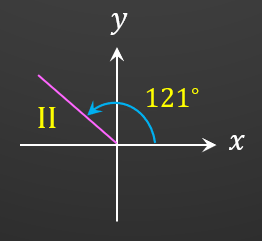
Quadrant II
θ = 180∘ – 59∘
= 121∘
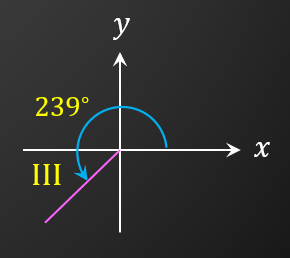
Quadrant III
θ = 180∘ + 59∘
= 239∘
(b)(i)
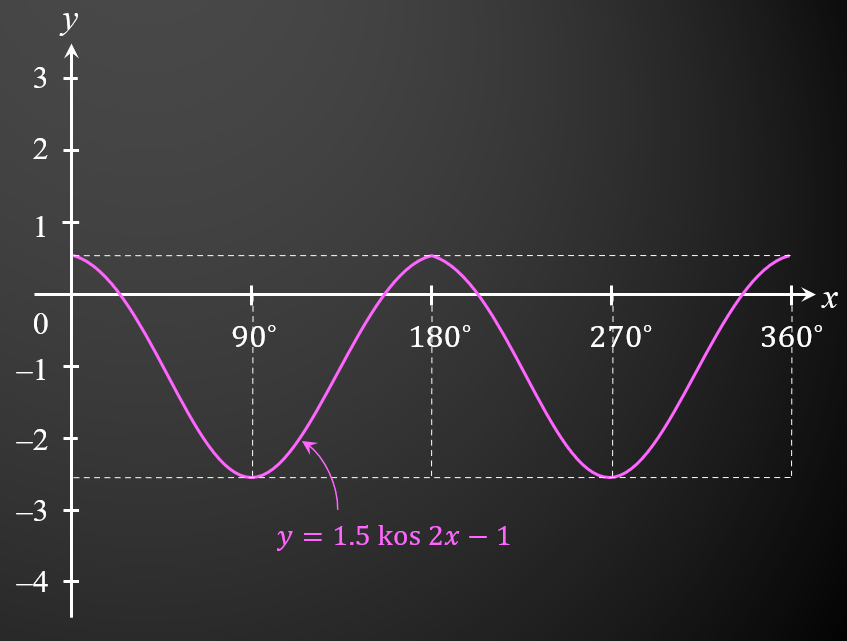
(b)(ii)
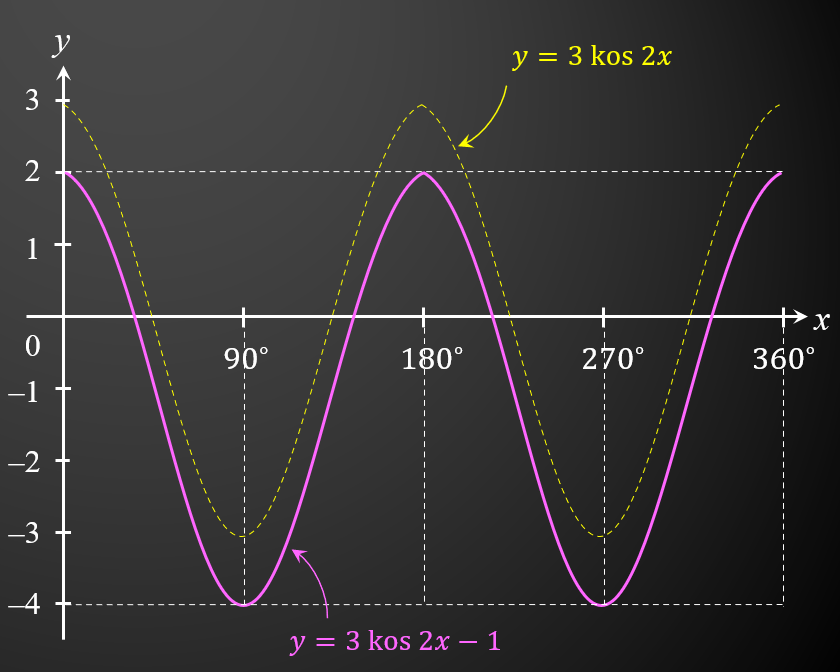
When the amplitude value is 3, the maximum point will be at y = 2 and the minimum point will be at y = -4.
$$ \text { (a) Transformation } \mathbf{M} \text { represents a translation }\binom{7}{-2} \text {. } $$
Transformation N represents reflection in the line y = x.
State the coordinate of the image of point (1, 4) under the combined transformation NM. [2 marks]
(b) Diagram 3 shows two Geometrical shapes, drawn on a Cartesian plane.
(i) State whether hexagon L and hexagon K are congruent. Justify your answer. [1 mark]
(ii) Hexagon L is the image of hexagon Kunder a transformation Q. Describe, in full, the transformation Q. [2 marks]
(a)
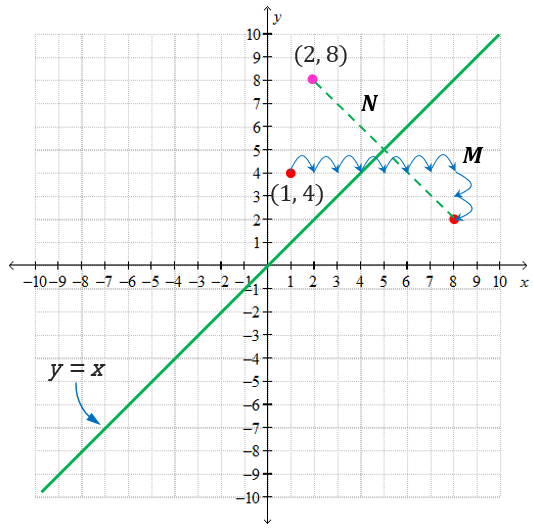
Coordinate of the image of point (1, 4) under the combined transformation NM is (2, 8)
(b)(i)
Yes, because measurement of all corresponding sides and angles are equal for both hexagons.
(b)(ii)
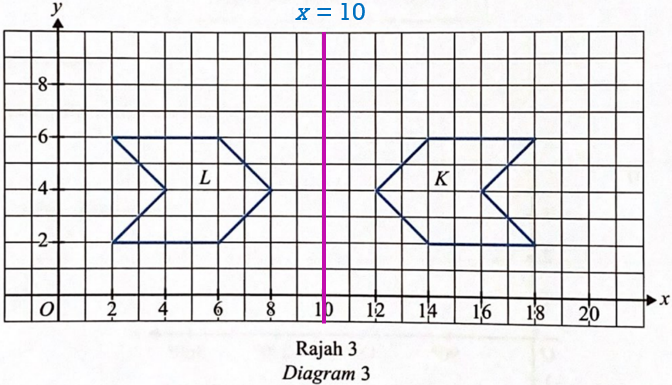
Transformation Q is reflection on the line x = 10.