Question 7:
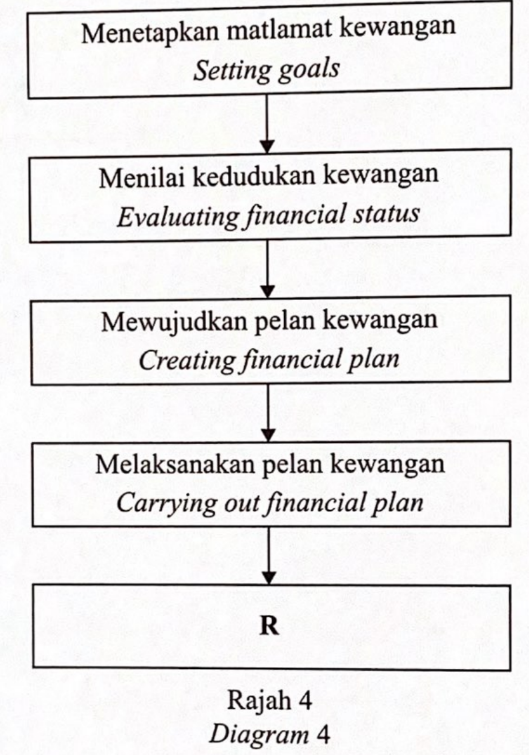
(a) Diagram 4 shows the incomplete steps in financial management process.
(b) Table 2 shows the income and expenses of Amelia and Julia in month of January.
Solution:
(a) R = Reviewing and revising the progress
(b)
Income = net salary, sales commission, rent received
Expenses = housing loan, utility bills, Insurance premium
$$ \begin{aligned} &\text { Financial position of Amelia }\\ &\begin{aligned} & =\mathrm{RM}(3500+400+800)-\mathrm{RM}(1300+650+200) \\ & =\text { RM4 } 700+\mathrm{RM} 2150 \\ & =\text { RM2 } 550 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Financial position of Julia }\\ &\begin{aligned} & =\text { RM }(3000+150+850)-R M(1800+700+300) \\ & =\text { RM4 } 000+\text { RM2 } 800 \\ & =\text { RM1 } 200 \end{aligned} \end{aligned} $$
(a) Diagram 4 shows the incomplete steps in financial management process.

State the step labelled R. [1 mark]
(b) Table 2 shows the income and expenses of Amelia and Julia in month of January.

Between Amelia and Julia, who has the best financial position? Justify your answer. [3 marks]
(a) R = Reviewing and revising the progress
(b)
Income = net salary, sales commission, rent received
Expenses = housing loan, utility bills, Insurance premium
$$ \begin{aligned} &\text { Financial position of Amelia }\\ &\begin{aligned} & =\mathrm{RM}(3500+400+800)-\mathrm{RM}(1300+650+200) \\ & =\text { RM4 } 700+\mathrm{RM} 2150 \\ & =\text { RM2 } 550 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Financial position of Julia }\\ &\begin{aligned} & =\text { RM }(3000+150+850)-R M(1800+700+300) \\ & =\text { RM4 } 000+\text { RM2 } 800 \\ & =\text { RM1 } 200 \end{aligned} \end{aligned} $$
Amelia has better financial position because surplus of income of Amelia is more than Julia.
Question 8:
Diagram 5 shows two ropes AE and BD tied in a parallel way to the vertical wooden pole EC.
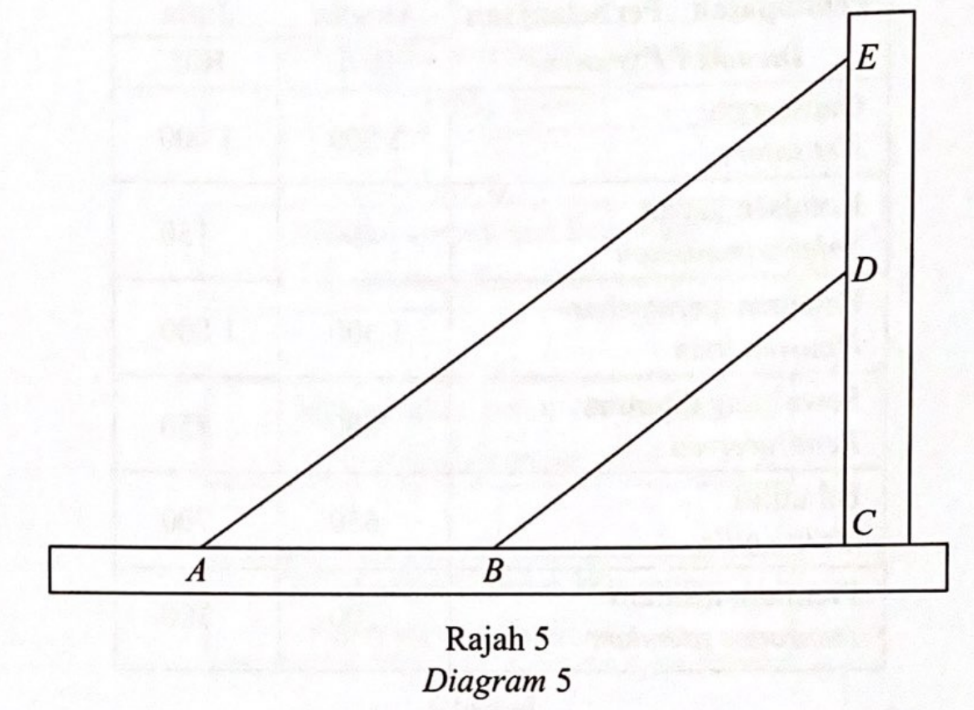 Given the equation of straight line BD is 4y – 3x = 48 and the ratio of distance AB : BC is 3 : 4.
Given the equation of straight line BD is 4y – 3x = 48 and the ratio of distance AB : BC is 3 : 4.
Find,
(a) the equation of the straight line AE, [3 marks]
(b) the distance of ED. [1 mark]
Solution:
(a)
$$ \begin{aligned} &\text { At point E, y coordinate } =0\\ &\begin{aligned} 4(0)-3 x & =48 \\ x & =-\frac{48}{3} \\ x & =-16 \end{aligned} \end{aligned} $$
$$ \text { Given that } \begin{aligned} \frac{A B}{B C} & =\frac{3}{4} \\ \frac{A B}{16} & =\frac{3}{4} \\ A B & =\frac{16 \times 3}{4} \\ A B & =12 \end{aligned} $$
$$ \begin{aligned} &\text { Thus, point } A\\ &\begin{aligned} & =(-16-12), 0) \\ & =(-28,0) \end{aligned} \end{aligned} $$
$$ \begin{aligned} 4 y-3 x & =48 \\ y & =\frac{3}{4} x+\frac{48}{4} \\ y & =\frac{3}{4} x+12 \\ m & =\frac{3}{4} \end{aligned} $$
$$ \begin{aligned} & m_{A E}=m_{B D}=\frac{3}{4} \\ & y=\frac{3}{4} x+c,(-28,0) \\ & 0=\frac{3}{4}(-28)+c \\ & c=21 \end{aligned} $$
$$ \begin{aligned} &\text { Equation of the straight line } A E \text {, }\\ &y=\frac{3}{4} x+21 \end{aligned} $$
(b)
$$ \text { y-intercept } of \text { the equation, } y=\frac{3}{4} x+12 \text { is } 12 $$
$$ \text { Thus, point } D=(0,12) $$
$$ \text { y-intercept } of \text { the equation, } y=\frac{3}{4} x+21 \text { is } 21 $$
$$ \text { Thus, point } E=(0,21) $$
$$ \begin{aligned} \text { Distance of } E D & =21-12 \\ & =9 \text { units } \end{aligned} $$
Diagram 5 shows two ropes AE and BD tied in a parallel way to the vertical wooden pole EC.
 Given the equation of straight line BD is 4y – 3x = 48 and the ratio of distance AB : BC is 3 : 4.
Given the equation of straight line BD is 4y – 3x = 48 and the ratio of distance AB : BC is 3 : 4.Find,
(a) the equation of the straight line AE, [3 marks]
(b) the distance of ED. [1 mark]
Solution:
(a)
$$ \begin{aligned} &\text { At point E, y coordinate } =0\\ &\begin{aligned} 4(0)-3 x & =48 \\ x & =-\frac{48}{3} \\ x & =-16 \end{aligned} \end{aligned} $$
$$ \text { Given that } \begin{aligned} \frac{A B}{B C} & =\frac{3}{4} \\ \frac{A B}{16} & =\frac{3}{4} \\ A B & =\frac{16 \times 3}{4} \\ A B & =12 \end{aligned} $$
$$ \begin{aligned} &\text { Thus, point } A\\ &\begin{aligned} & =(-16-12), 0) \\ & =(-28,0) \end{aligned} \end{aligned} $$
$$ \begin{aligned} 4 y-3 x & =48 \\ y & =\frac{3}{4} x+\frac{48}{4} \\ y & =\frac{3}{4} x+12 \\ m & =\frac{3}{4} \end{aligned} $$
$$ \begin{aligned} & m_{A E}=m_{B D}=\frac{3}{4} \\ & y=\frac{3}{4} x+c,(-28,0) \\ & 0=\frac{3}{4}(-28)+c \\ & c=21 \end{aligned} $$
$$ \begin{aligned} &\text { Equation of the straight line } A E \text {, }\\ &y=\frac{3}{4} x+21 \end{aligned} $$
(b)
$$ \text { y-intercept } of \text { the equation, } y=\frac{3}{4} x+12 \text { is } 12 $$
$$ \text { Thus, point } D=(0,12) $$
$$ \text { y-intercept } of \text { the equation, } y=\frac{3}{4} x+21 \text { is } 21 $$
$$ \text { Thus, point } E=(0,21) $$
$$ \begin{aligned} \text { Distance of } E D & =21-12 \\ & =9 \text { units } \end{aligned} $$