Question 9:
SMK Ria Idaman will hold a retirement ceremony for a teacher by decorating a stage. Diagram 6 shows the floor plan of the stage and the area to be decorated. The stage is in rectangular shape. Two quarter circles each centered at C and F respectively will be placed with ornamental grass.
Solution:
(a)
$$ \text { Given that } \begin{aligned} F G & =\frac{2}{5} C D \\ & =\frac{2}{5}(12 \mathrm{~m}) \\ & =\frac{24}{5} \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \text { Length }_{E G} & =\frac{\theta}{360} \times 2 \pi r \\ & =\frac{90}{360} \times 2 \times \frac{22}{7} \times \frac{24}{5} \\ & =\frac{264}{35} \\ & =7 \frac{19}{35} \mathrm{~m} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Area of circle }=\frac{\theta}{360} \times \pi r^2 \\ & A_{E F G}=\frac{90}{360} \times \frac{22}{7} \times\left(\frac{24}{5}\right)^2 \\ & =\frac{3168}{175} \mathrm{~m}^2 \\ & A_{B C D}=\frac{90}{360} \times \frac{22}{7} \times 12^2 \\ & =\frac{792}{7} \mathrm{~m}^2 \end{aligned} $$
The area that will be covered with ornamental grass $$ \begin{aligned} & =\frac{3168}{175}+\frac{792}{7} \\ & =131 \frac{43}{175} \mathrm{~m}^2 \end{aligned} $$
SMK Ria Idaman will hold a retirement ceremony for a teacher by decorating a stage. Diagram 6 shows the floor plan of the stage and the area to be decorated. The stage is in rectangular shape. Two quarter circles each centered at C and F respectively will be placed with ornamental grass.

Given that the length of AB = 12 m and B is the midpoint of AC while the length of FG = 2/5 CD.
Using π = 22/7, calculate
(a) the length, in m , of arc EG, [2 marks]
(b) the area, in m2, that will be covered with ornamental grass. [2 marks]
Solution:
(a)
$$ \text { Given that } \begin{aligned} F G & =\frac{2}{5} C D \\ & =\frac{2}{5}(12 \mathrm{~m}) \\ & =\frac{24}{5} \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \text { Length }_{E G} & =\frac{\theta}{360} \times 2 \pi r \\ & =\frac{90}{360} \times 2 \times \frac{22}{7} \times \frac{24}{5} \\ & =\frac{264}{35} \\ & =7 \frac{19}{35} \mathrm{~m} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Area of circle }=\frac{\theta}{360} \times \pi r^2 \\ & A_{E F G}=\frac{90}{360} \times \frac{22}{7} \times\left(\frac{24}{5}\right)^2 \\ & =\frac{3168}{175} \mathrm{~m}^2 \\ & A_{B C D}=\frac{90}{360} \times \frac{22}{7} \times 12^2 \\ & =\frac{792}{7} \mathrm{~m}^2 \end{aligned} $$
The area that will be covered with ornamental grass $$ \begin{aligned} & =\frac{3168}{175}+\frac{792}{7} \\ & =131 \frac{43}{175} \mathrm{~m}^2 \end{aligned} $$
Question 10:
Table 3 shows data obtained from a survey of 50 pupils on the type of music they like.
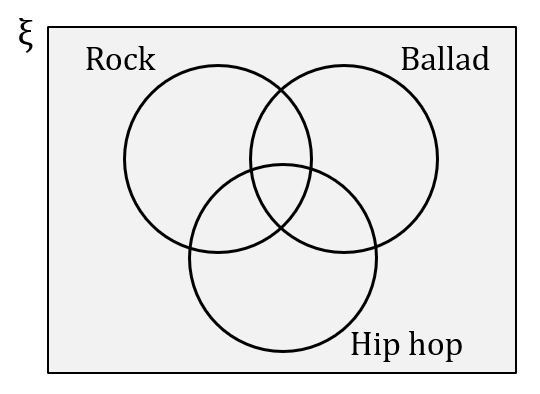
(a) Given the number of pupils who like ballads only is twice the number of pupils who like hip hop only. Complete the Venn diagram in the answer space. [2 marks]
Solution:
(a)
(b)
(c)
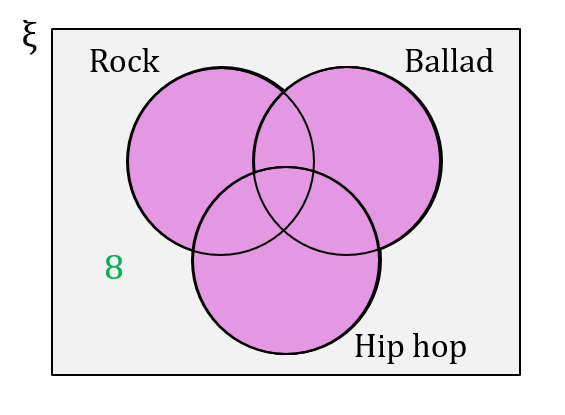 Pupils who do not like any music = 8
Pupils who do not like any music = 8
Table 3 shows data obtained from a survey of 50 pupils on the type of music they like.

(a) Given the number of pupils who like ballads only is twice the number of pupils who like hip hop only. Complete the Venn diagram in the answer space. [2 marks]

(b) Hence,
(i) calculate the number of pupils who like rock or hip hop music but not ballad, [1 mark]
(ii) pupils who do not like any music. [1 mark]
Solution:
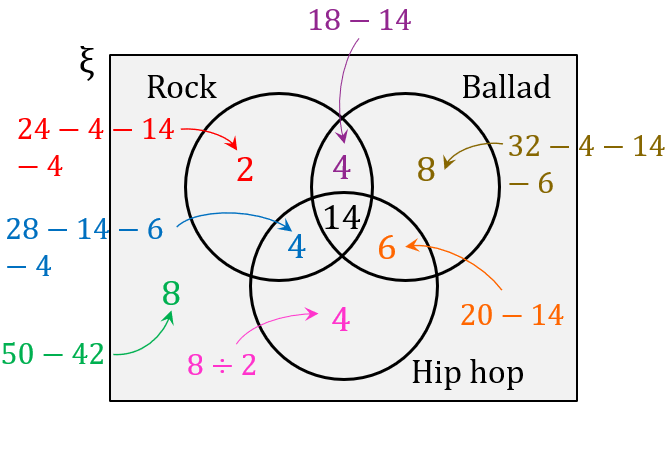
(a)

(b)

The number of pupils who like rock or hip hop music but not ballad,
$$
\begin{aligned}
n\left(R \cup H \cap B^{\prime}\right) & =2+4+4 \\
& =10
\end{aligned}
$$
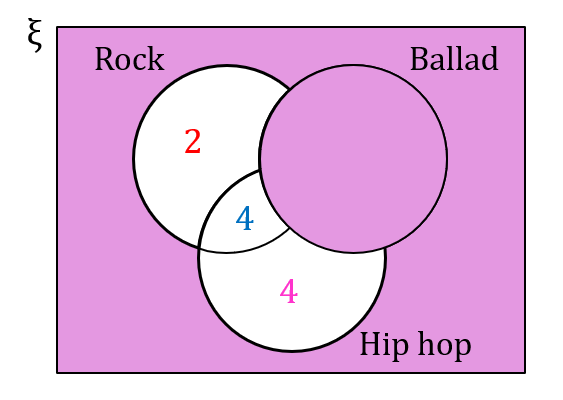
(c)
 Pupils who do not like any music = 8
Pupils who do not like any music = 8