Question 16(a):
Sirhan is an archery coach.
(a) Sirhan is preparing a field for archery. He wants to construct two perpendicular lines using three posts and string. Diagram 10 shows a plan of the archery field with the three posts P, Q and R.
Based on Diagram 10,
(i) name the shape formed by the three posts, [1 mark]
(ii) calculate the distance, in m, between post P and post R if PQ = 2.5 m dan QR = 6.0 m. [2 marks]
Solution:
(a)(i)
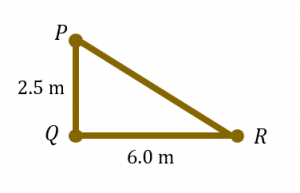Shape formed by the three posts is a right-angled triangle.
(a)(ii)
$$ \begin{aligned} &\text { Distance between post } P \text { and post } R\\ &\begin{aligned} & =\sqrt{2.5^2+6^2} \\ & =6.5 \mathrm{~m} \end{aligned} \end{aligned} $$
Sirhan is an archery coach.
(a) Sirhan is preparing a field for archery. He wants to construct two perpendicular lines using three posts and string. Diagram 10 shows a plan of the archery field with the three posts P, Q and R.
Based on Diagram 10,(i) name the shape formed by the three posts, [1 mark]
(ii) calculate the distance, in m, between post P and post R if PQ = 2.5 m dan QR = 6.0 m. [2 marks]
Solution:
(a)(i)
Shape formed by the three posts is a right-angled triangle.(a)(ii)
$$ \begin{aligned} &\text { Distance between post } P \text { and post } R\\ &\begin{aligned} & =\sqrt{2.5^2+6^2} \\ & =6.5 \mathrm{~m} \end{aligned} \end{aligned} $$
Question 16(b):
$$ \begin{aligned} P(z) & =\frac{3}{5} \\ P\left(z^{\prime}\right) & =1-\frac{3}{5} \\ & =\frac{2}{5} \end{aligned} $$
$$ \begin{aligned} P(s) & =\frac{4}{9} \\ P\left(s^{\prime}\right) & =1-\frac{4}{9} \\ & =\frac{5}{9} \end{aligned} $$
$$ \begin{aligned} & P \text { (Zarif or Syafi move to second round) } \\ & =1-P(\text { both Zarif and Syafi do not move to } \\ & \quad \text { second round) } \\ & =1-P\left(z^{\prime}\right) P\left(s^{\prime}\right) \\ & =1-\left(\frac{2}{5} \times \frac{5}{9}\right) \\ & =\frac{7}{9} \end{aligned} $$
Two of Sirhan’s trainees, Zarif and Syafi are competing in the early round of an archery competition. It is given that the probability that Zarif manages to move to the second round is 3/5 and the probability that Syafi manages to move to the second round is 4/9.
Find the probability that Zarif or Syafi manages to move to the second round of the competition.
[3 marks]
$$ \begin{aligned} P(z) & =\frac{3}{5} \\ P\left(z^{\prime}\right) & =1-\frac{3}{5} \\ & =\frac{2}{5} \end{aligned} $$
$$ \begin{aligned} P(s) & =\frac{4}{9} \\ P\left(s^{\prime}\right) & =1-\frac{4}{9} \\ & =\frac{5}{9} \end{aligned} $$
$$ \begin{aligned} & P \text { (Zarif or Syafi move to second round) } \\ & =1-P(\text { both Zarif and Syafi do not move to } \\ & \quad \text { second round) } \\ & =1-P\left(z^{\prime}\right) P\left(s^{\prime}\right) \\ & =1-\left(\frac{2}{5} \times \frac{5}{9}\right) \\ & =\frac{7}{9} \end{aligned} $$
Question 16(c):
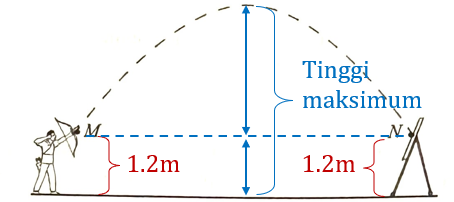
(c) A boy has shot an arrow. Diagram 11 shows the path of the arrow from point M to point N.
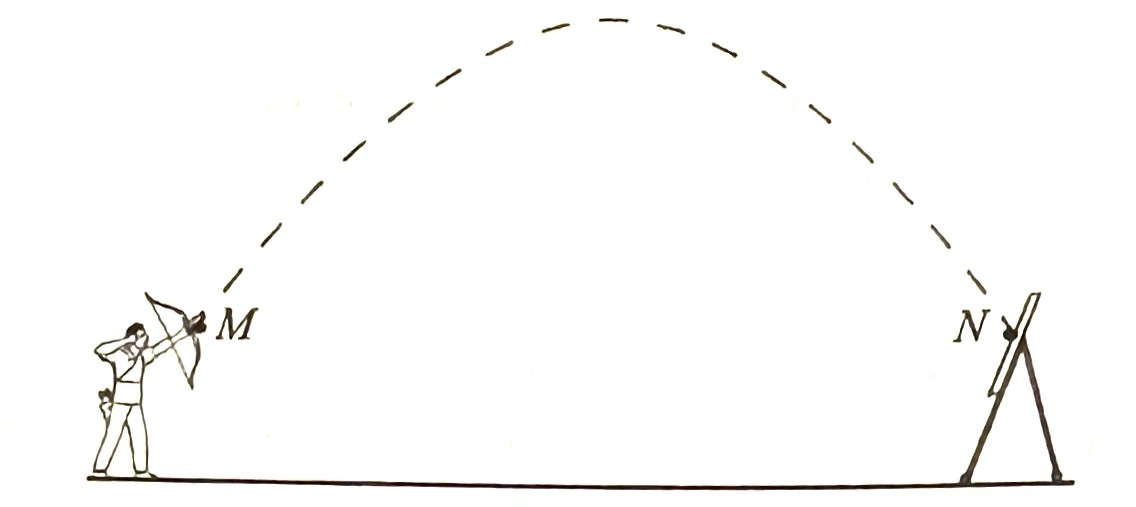
Solution:
$$
f(x)=-\frac{13}{200} x^2+\frac{39}{20} x
$$
$$ \begin{aligned} x & =-\frac{b}{2 a} \\ & =-\frac{\left(\frac{39}{20}\right)}{2\left(-\frac{13}{200}\right)} \\ & =-\frac{39}{20} \times-\frac{100}{13} \\ & =15 \end{aligned} $$
$$ \begin{aligned} f(15) & =-\frac{13}{200}(15)^2+\frac{39}{20}(15) \\ & =14.625 \end{aligned} $$
$$ \begin{aligned} \text { Maximum height } & =14.625 \mathrm{~m}+1.2 \mathrm{~m} \\ & =15.825 \mathrm{~m} \end{aligned} $$
(c) A boy has shot an arrow. Diagram 11 shows the path of the arrow from point M to point N.
Point M and point N are 1.2 m vertically above the horizontal ground. The path of the arrow can be represented by the quadratic function, $$
f(x)=\frac{13}{200} x^2+\frac{39}{20} x
$$
Calculate the maximum height, in m, reached by the arrow as measured from the ground.
[5 marks]
Solution:
$$
f(x)=-\frac{13}{200} x^2+\frac{39}{20} x
$$$$ \begin{aligned} x & =-\frac{b}{2 a} \\ & =-\frac{\left(\frac{39}{20}\right)}{2\left(-\frac{13}{200}\right)} \\ & =-\frac{39}{20} \times-\frac{100}{13} \\ & =15 \end{aligned} $$
$$ \begin{aligned} f(15) & =-\frac{13}{200}(15)^2+\frac{39}{20}(15) \\ & =14.625 \end{aligned} $$
$$ \begin{aligned} \text { Maximum height } & =14.625 \mathrm{~m}+1.2 \mathrm{~m} \\ & =15.825 \mathrm{~m} \end{aligned} $$
Question 16(d):
Sirhan records the scores for Zarif and the scores for Syafi. He calculates the mean and the standard deviation of the scores for Zarif which are 7.542 and 1.233 respectively. Table 10 shows the score distribution for Syafi.
By calculating the mean and the standard deviation for Syafi, compare the performances of the two archers. You should comment on which archer performs better on average and which archer is more consistent. [4 marks]
Solution:
$$ \begin{aligned} \text { Mean, } \bar{x} \text { for Syafi } & =\frac{\sum f x}{\Sigma f} \\ & =\frac{19(6)+21(7)+24(8)+6(9)+2(10)}{19+21+24+6+2} \\ & =\frac{527}{72} \\ & =7.319 \end{aligned} $$
Mean for Zarif is 7.542, so Zarif performs better on average.
$$ \begin{aligned} & \text { Standard deviation for Syafi }=\sqrt{\frac{\Sigma f x^2}{\Sigma f}-\bar{x}^2} \\ & \begin{aligned} \sigma & =\sqrt{\frac{19(6)^2+21(7)^2+24(8)^2+6(9)^2+2(10)^2}{72}-7.319^2} \\ & =\sqrt{\frac{3935}{72}-7.319^2} \\ & =1.042 \end{aligned} \end{aligned} $$
$$ \text { Standard deviation of the scores for Zarif is 1.233. In this case, Syafi is more consistent. } $$
Sirhan records the scores for Zarif and the scores for Syafi. He calculates the mean and the standard deviation of the scores for Zarif which are 7.542 and 1.233 respectively. Table 10 shows the score distribution for Syafi.
By calculating the mean and the standard deviation for Syafi, compare the performances of the two archers. You should comment on which archer performs better on average and which archer is more consistent. [4 marks]
Solution:
$$ \begin{aligned} \text { Mean, } \bar{x} \text { for Syafi } & =\frac{\sum f x}{\Sigma f} \\ & =\frac{19(6)+21(7)+24(8)+6(9)+2(10)}{19+21+24+6+2} \\ & =\frac{527}{72} \\ & =7.319 \end{aligned} $$
Mean for Zarif is 7.542, so Zarif performs better on average.
$$ \begin{aligned} & \text { Standard deviation for Syafi }=\sqrt{\frac{\Sigma f x^2}{\Sigma f}-\bar{x}^2} \\ & \begin{aligned} \sigma & =\sqrt{\frac{19(6)^2+21(7)^2+24(8)^2+6(9)^2+2(10)^2}{72}-7.319^2} \\ & =\sqrt{\frac{3935}{72}-7.319^2} \\ & =1.042 \end{aligned} \end{aligned} $$
$$ \text { Standard deviation of the scores for Zarif is 1.233. In this case, Syafi is more consistent. } $$