Question 15:
$$ \text { (a) It is given that }\left[\begin{array}{cc} 7 & -2 \\ x+3 & 4 \end{array}\right]=\left[\begin{array}{cc} 7 & 5 y \\ -1 & 4 \end{array}\right] \text {. } $$
Solution:
(a)
$$ \begin{aligned} {\left[\begin{array}{cc} 7 & -2 \\ x+3 & 4 \end{array}\right] } & =\left[\begin{array}{cc} 7 & 5 y \\ -1 & 4 \end{array}\right] \\ x+3 & =-1 \\ x & =-4 \\ 5 y & =-2 \\ y & =-\frac{2}{5} \end{aligned} $$
(b)(i)
$$ \begin{aligned} &3 x+2 y=55 \sim \text { (Lily) }\\ &\begin{aligned} & 4 x+3 y=55+20 \sim \text { (Kelly) } \\ & 4 x+3 y=75 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & {\left[\begin{array}{ll} 3 & 2 \\ 4 & 3 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} 55 \\ 75 \end{array}\right]} \\ & {\left[\begin{array}{l} x \\ y \end{array}\right]=\frac{1}{(3)(3)-(2)(4)}\left[\begin{array}{cc} 3 & -2 \\ -4 & 3 \end{array}\right]\left[\begin{array}{l} 55 \\ 75 \end{array}\right]} \\ & {\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} (3 \times 55)+(-2 \times 75) \\ (-4 \times 55)+(3 \times 75) \end{array}\right]} \\ & {\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{c} 165-150 \\ -220+225 \end{array}\right]} \\ & {\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{c} 15 \\ 5 \end{array}\right]} \\ & \text { A box of sushi }=\text { RM15 } \\ & \text { A piece of fried chicken = RM5 } \end{aligned} $$
(b)(ii)
$$ \text { A box of sushi at discounted price }=15 \times \frac{80}{100}=\text { RM12 } $$
$$ \text { A piece of fried chicken at discounted price }=5 \times \frac{60}{100}=\text { RM3 } $$
$$ \begin{aligned} &2 \text { boxes of sushi and } 8 \text { pieces of fried chicken in matrix multiplication }\\ &\begin{aligned} & =\left[\begin{array}{ll} 2 & 8 \end{array}\right]\left[\begin{array}{c} 12 \\ 3 \end{array}\right] \\ & =[2 \times 12+8 \times 3] \\ & =[48] \end{aligned} \end{aligned} $$
$$ \text { Therefore, Jane has enough money as only RM48 is needed. } $$
$$ \text { (a) It is given that }\left[\begin{array}{cc} 7 & -2 \\ x+3 & 4 \end{array}\right]=\left[\begin{array}{cc} 7 & 5 y \\ -1 & 4 \end{array}\right] \text {. } $$
Determine the value of x and of y. [2 marks]
(b) A supermarket sells boxes of sushi and pieces of fried chicken.
(i) Lily spent RM55 on 3 boxes of sushi and 2 pieces of fried chicken. Kelly spent RM20 more compared to Lily on 4 boxes of sushi and 3 pieces of fried chicken. Using matrix method, calculate the price of a box of sushi and of a piece of fried chicken. [5 marks]
(ii) Diagram 9 shows the discounts given by the supermarket on a particular day.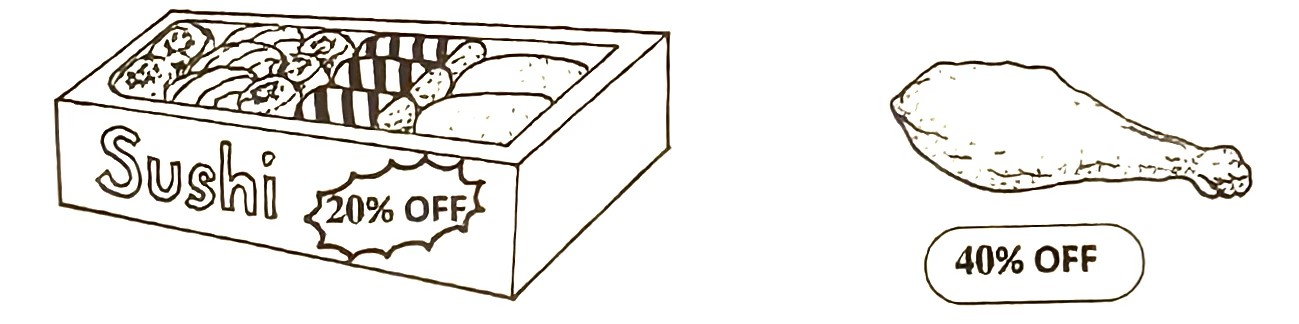
Jane has RM50. She wants to buy 2 boxes of sushi and 8 pieces of fried chicken. Does she have enough money to buy these items at the discounted price? Justify your answer by using matrix multiplication. [3 marks]
Solution:
(a)
$$ \begin{aligned} {\left[\begin{array}{cc} 7 & -2 \\ x+3 & 4 \end{array}\right] } & =\left[\begin{array}{cc} 7 & 5 y \\ -1 & 4 \end{array}\right] \\ x+3 & =-1 \\ x & =-4 \\ 5 y & =-2 \\ y & =-\frac{2}{5} \end{aligned} $$
(b)(i)
$$ \begin{aligned} &3 x+2 y=55 \sim \text { (Lily) }\\ &\begin{aligned} & 4 x+3 y=55+20 \sim \text { (Kelly) } \\ & 4 x+3 y=75 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & {\left[\begin{array}{ll} 3 & 2 \\ 4 & 3 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} 55 \\ 75 \end{array}\right]} \\ & {\left[\begin{array}{l} x \\ y \end{array}\right]=\frac{1}{(3)(3)-(2)(4)}\left[\begin{array}{cc} 3 & -2 \\ -4 & 3 \end{array}\right]\left[\begin{array}{l} 55 \\ 75 \end{array}\right]} \\ & {\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} (3 \times 55)+(-2 \times 75) \\ (-4 \times 55)+(3 \times 75) \end{array}\right]} \\ & {\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{c} 165-150 \\ -220+225 \end{array}\right]} \\ & {\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{c} 15 \\ 5 \end{array}\right]} \\ & \text { A box of sushi }=\text { RM15 } \\ & \text { A piece of fried chicken = RM5 } \end{aligned} $$
(b)(ii)
$$ \text { A box of sushi at discounted price }=15 \times \frac{80}{100}=\text { RM12 } $$
$$ \text { A piece of fried chicken at discounted price }=5 \times \frac{60}{100}=\text { RM3 } $$
$$ \begin{aligned} &2 \text { boxes of sushi and } 8 \text { pieces of fried chicken in matrix multiplication }\\ &\begin{aligned} & =\left[\begin{array}{ll} 2 & 8 \end{array}\right]\left[\begin{array}{c} 12 \\ 3 \end{array}\right] \\ & =[2 \times 12+8 \times 3] \\ & =[48] \end{aligned} \end{aligned} $$
$$ \text { Therefore, Jane has enough money as only RM48 is needed. } $$