SPM Mathematics Trial 2021 (Selangor), Paper 2 (Question 16)

Question 16 (15 marks):
The Venn diagram below shows a representation of 42 students of Usahawan Tani Club at a school who are fond of three types of local fruits, watermelon, guava and pineapple.


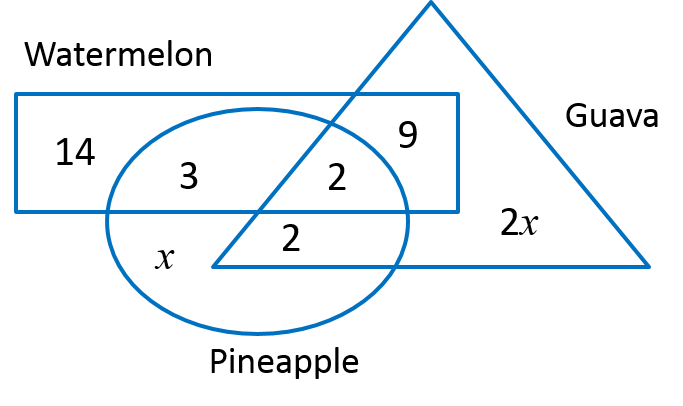
(a) Given the number of students who like guava only is twice the number of students who like pineapple only.
Calculate:
(i) the number of students who like guava. 
(ii) the number of students who like two types of local fruit. 
[5 marks]


Solution:
(a)(i)

$\begin{array}{l}14+3+2+9+2x+x+2=42\\ 30+3x=42\\ 3x=12\\ x=4\\ \\ \text{Number of students who like guava}\\ =2+2+9+2(4)\\ =21\end{array}$

(a)(ii)

$\begin{array}{l}\text{Number of students who like two types of local fruit}\\ =3+9+2\\ =14\end{array}$

(b) On Annual Carnival Day, Usahawan Tani Club held a sale of watermelon juice and guava juice. Both drinks are sold in small glasses and large glasses. The club has managed to sell 52 small glasses and 35 large glasses of watermelon juice. While managed to sell 40 small glasses and 32 large glasses of guava juice. The total sales obtained from the sale of watermelon juice and guava juice were RM392 and RM332 respectively.

(i) Construct two linear equations from the above situation.
(ii) By using the matrix method, calculate the price of a small glass and the price of a large glass.
[6 marks]


Solution:
(b)(i)
Let x represents small glass and y represents large glass.
Thus,
52x + 35y = 392
40x + 32y = 332

(b)(ii)

$\begin{array}{l}\left(\begin{array}{l}52\text{ 35}\\ 40\text{ 32}\end{array}\right)\left(\begin{array}{l}x\\ y\end{array}\right)=\left(\begin{array}{l}392\\ 332\end{array}\right)\\ \\ \left(\begin{array}{l}x\\ y\end{array}\right)=\frac{1}{52\left(32\right)-35\left(40\right)}\left(\begin{array}{l}\text{ 32}-35\\ -40\text{ 52}\end{array}\right)\left(\begin{array}{l}392\\ 332\end{array}\right)\\ \\ \left(\begin{array}{l}x\\ y\end{array}\right)=\frac{1}{264}\left(\begin{array}{l}32\left(392\right)+\left(-35\right)\left(332\right)\\ -40\left(392\right)+52\left(332\right)\end{array}\right)\\ \\ \left(\begin{array}{l}x\\ y\end{array}\right)=\frac{1}{264}\left(\begin{array}{l}924\\ \text{1584}\end{array}\right)\\ \\ \left(\begin{array}{l}x\\ y\end{array}\right)=\left(\begin{array}{l}3.5\\ 6\end{array}\right)\\ \\ x=3.5\text{ and }y=6\\ \\ \text{Thus, price of a small glass = RM3}\text{.50,}\\ \text{and price of a large glass = RM6}\text{.00}\text{. }\end{array}$

(c)
The school has obtained a piece of land to be cultivated by the Usahawan Tani Club. The club has planned to plant all three of their favourite local fruit varities. Diagram 9 shows a piece of land that is rectangular in shape PSTU.


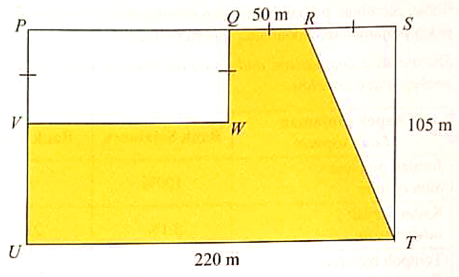
The rectangular land area PQWV will be planted with watermelon fruits, the triangle RST will be planted with guava fruits and the remaining area will be planted with pineapple fruits.
Calculate the land area, in m², to be planted with pineapple fruits.
[4 marks]

Solution:

$\begin{array}{l}\text{Area of rectangular shape }PQWV\\ =PQ\times QW\\ =\left(220-50-50\right)\times 50\\ =120\times 50\\ =6000{\text{ m}}^{\text{2}}\\ \\ \text{Area of triangle }RST\\ =\frac{1}{2}\times 50\times 105\\ =2625{\text{ m}}^{\text{2}}\\ \\ \text{Area planted with pineapples}\\ =\left(220\times 105\right)-6000-2625\\ =23100-6000-2625\\ =14475{\text{ m}}^{\text{2}}\end{array}$