SPM Mathematics Trial 2021 (Kelantan), Paper 2 (Question 1 & 2)

                                                              Section A
                                                              40 marks
                                                   Answer all questions

Question 1 (4 marks):
Diagram 1 shows a Cartesian plane.
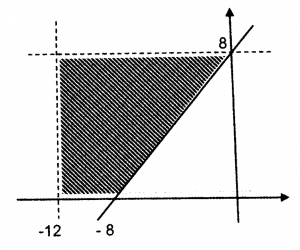Diagram 1
Write four inequalities that define the shaded region.

Answer:
(i)
(ii)
(iii)
(iv)

Solution:

(i)
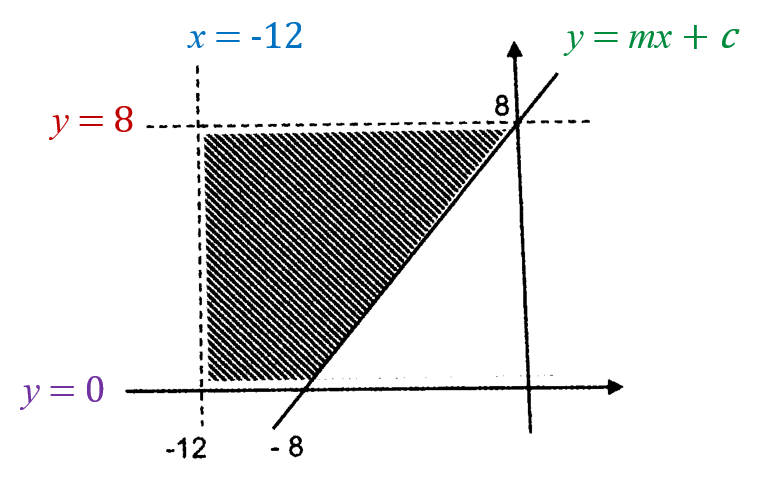
For y = 8
The inequality of the shaded region below the dashed line is y < 8.


(ii)
For x = -12
The inequality of the shaded region on the right of the dashed line is x > -12.

(iii)
For y = 0
The inequality of the shaded region above the x-axis is y ≥ 0.

(iv)
$\begin{array}{l}y=mx+c\\ c=8\\ \\ m=-\frac{8}{-8}=1\\ \therefore y=x+8\end{array}$

The inequality of the shaded region above the solid line is y ≥ x + 8.

Question 2 (4 marks):
Given the area of a triangle, A, varies directly with the constant, k, with height, x cm and base, y cm. Rajoo has a triangular-shaped piece of cardboard with x and y are 80 cm and 48 cm respectively. Calculate the value of k if the area of the cardboard is 15 360 cm². Next calculate the value of A if Rajoo has another piece of cardboard with the sum of x and y is 180 cm where the ratio of x to y is 5 : 4.

Solution:
A α xy
A = kxy

A = 15 360, x = 80, y = 48
15 360 = k × 80 × 48
15 360 = 3 840 k 
k = 4

x + y = 180
x : y = 5 : 4

$\begin{array}{l}x=\frac{\text{5}}{\text{9}}\times 180\\ =100\\ \\ y=\frac{\text{4}}{\text{9}}\times 180\\ =80\\ \\ \therefore A=4\times 100\times 80\\ =32000\end{array}$