Question 13:
(a) Diagram 7.1 shows point K on a Cartesian plane.
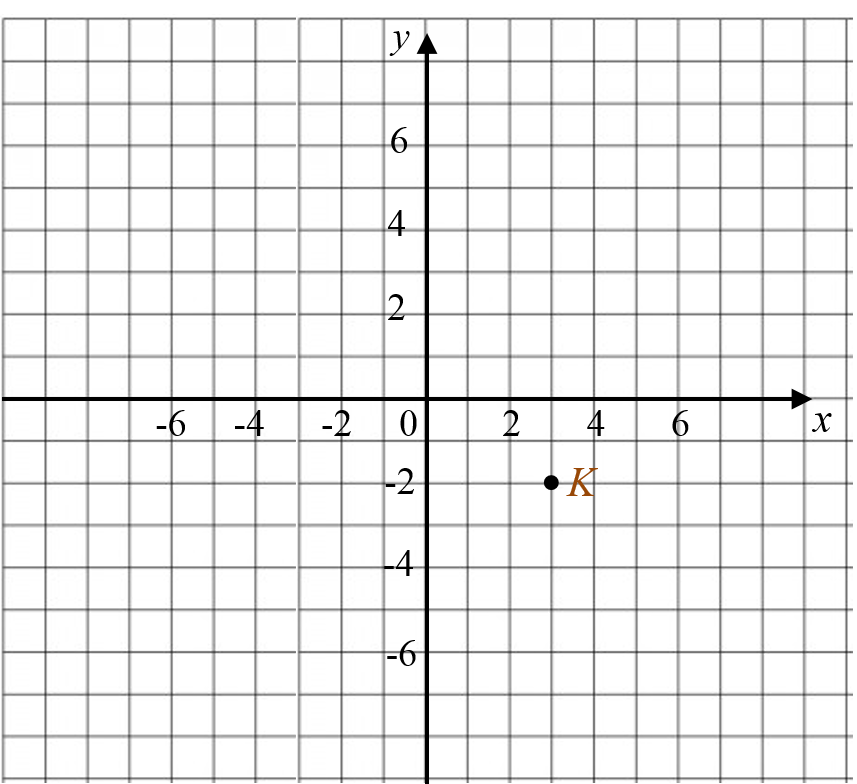Diagram 7.1
(b) Diagram 7.2 shows three pentagons EFGHJ, KLMNP, and KQRST, drawn on a Cartesian plane.
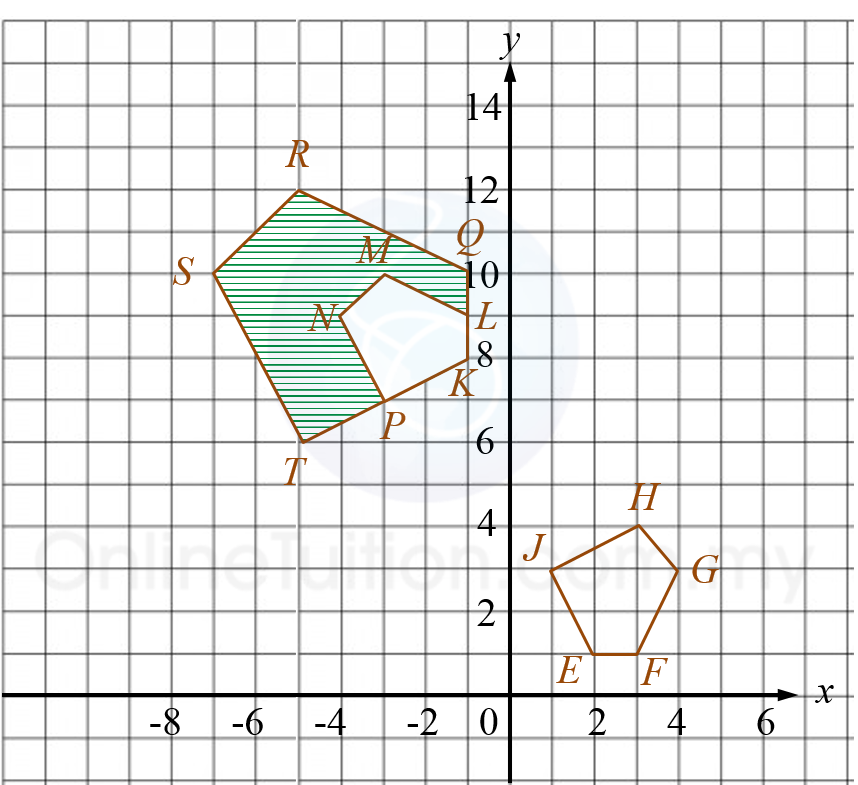Diagram 7.2
(i) Pentagon KQRST is the image of pentagon EFGHJ under the combined transformation VU.
Describe, in full, the transformation:
(a) U, (b) V.
(ii) It is given that the pentagon KQRST represents a region of area 288 m2.
Calculate the area, in m2, of the shaded region.
[9 marks].
Solution:
(a)
(a)(i)
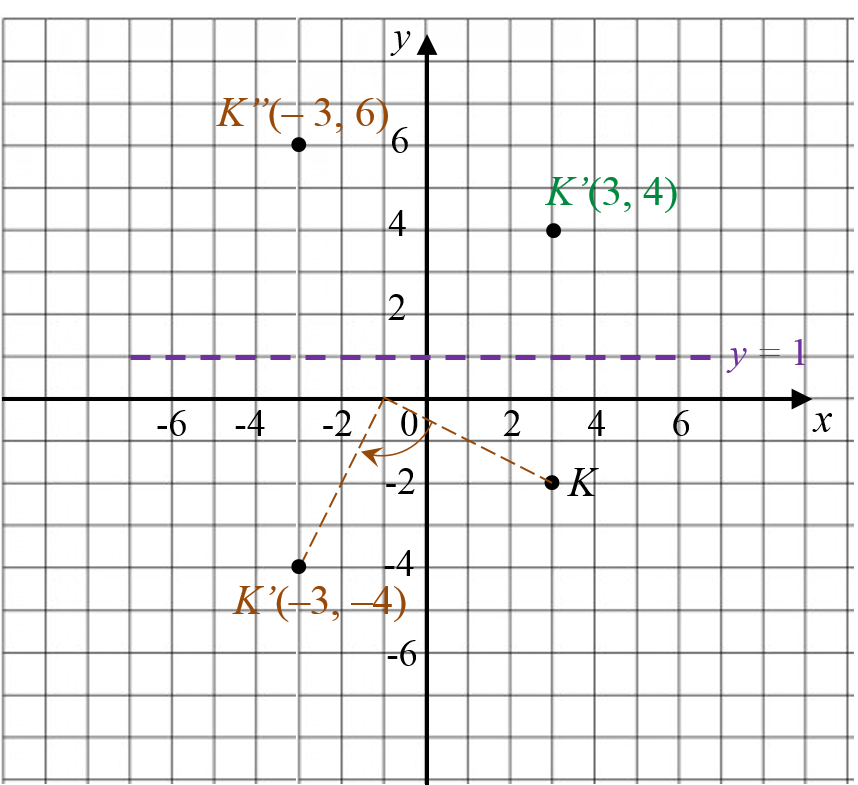
Point K (3, –2) is reflected in the line y = 1.
K (3, –2) → P → K’ (3, 4).
Coordinates of image are (3, 4).
(a)(ii)
K (3, –2) → R → K’ (–3, –4) → P → K’’ (–3, 6).
Coordinates of image are (–3, 6).
(b)
(b)(i)(a)
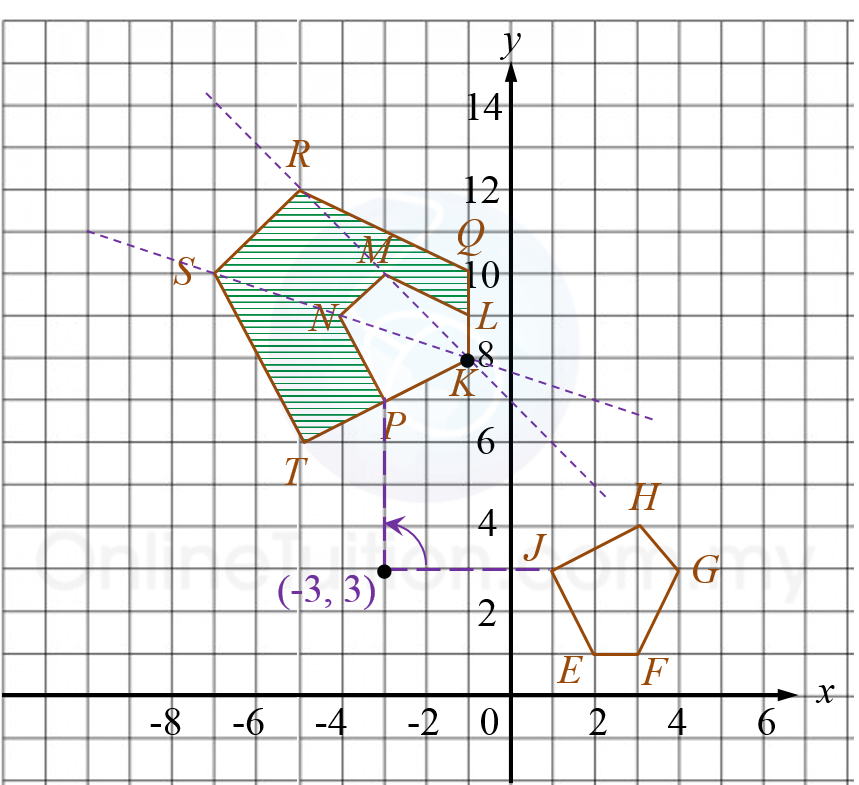
U: 90o rotation in clockwise direction at centre (–3, 3).
(b)(i)(a)
V: enlargement at centre K(–1, 8) with scale factor 2.
(b)(ii)
Area of KQRST = (scale factor)2 × Area of KLMNP
288 = 22 × Area of KLMNP
Area of KLMNP = 72 m2
Area of shaded region
= Area of KQRST – Area of KLMNP
= 288 m2 – 72 m2
= 216 m2
(a) Diagram 7.1 shows point K on a Cartesian plane.
Diagram 7.1 Diagram 7.1 shows point K on a Cartesian plane.
Transformation P is a reflection in the line y = 1.
Transformation R is a clockwise rotation of 90° about the centre (-1,0)
State the coordinates of the image of point K under each of the following transformations:
(i) P,
(ii) PR.
[3 marks]
(b) Diagram 7.2 shows three pentagons EFGHJ, KLMNP, and KQRST, drawn on a Cartesian plane.
Diagram 7.2(i) Pentagon KQRST is the image of pentagon EFGHJ under the combined transformation VU.
Describe, in full, the transformation:
(a) U, (b) V.
(ii) It is given that the pentagon KQRST represents a region of area 288 m2.
Calculate the area, in m2, of the shaded region.
[9 marks].
Solution:
(a)
(a)(i)
Point K (3, –2) is reflected in the line y = 1.
K (3, –2) → P → K’ (3, 4).
Coordinates of image are (3, 4).
(a)(ii)
K (3, –2) → R → K’ (–3, –4) → P → K’’ (–3, 6).
Coordinates of image are (–3, 6).
(b)
(b)(i)(a)
U: 90o rotation in clockwise direction at centre (–3, 3).
(b)(i)(a)
V: enlargement at centre K(–1, 8) with scale factor 2.
(b)(ii)
Area of KQRST = (scale factor)2 × Area of KLMNP
288 = 22 × Area of KLMNP
Area of KLMNP = 72 m2
Area of shaded region
= Area of KQRST – Area of KLMNP
= 288 m2 – 72 m2
= 216 m2