Question 15 (12 marks):
You are not allowed to use graph paper to answer this question.
(a) Diagram 11.1 shows a solid prism with a rectangular base JKLM on a horizontal plane. The surface MQRSTL is the uniform cross section of the prism. Triangle STU and PQR are horizontal planes. Edges PJ, RS and UK are vertical. PQ = TU = 3 cm.
Diagram 11.1
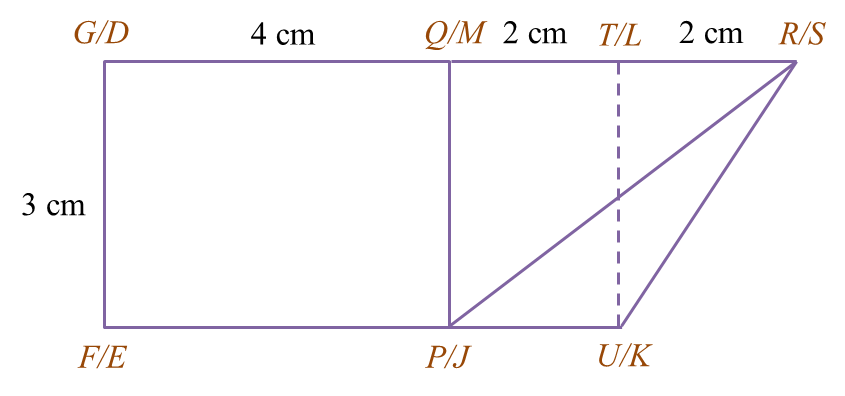
Draw to full scale, the elevation of the solid on a vertical plane parallel to KL as viewed from X.
(b) Another solid cuboid with rectangle base JMDE is combined to the prism in Diagram 11.1 at the vertical plane JMQP. The composite solid is as shown in Diagram 11.2. The base EJKLMD lies on a horizontal plane.
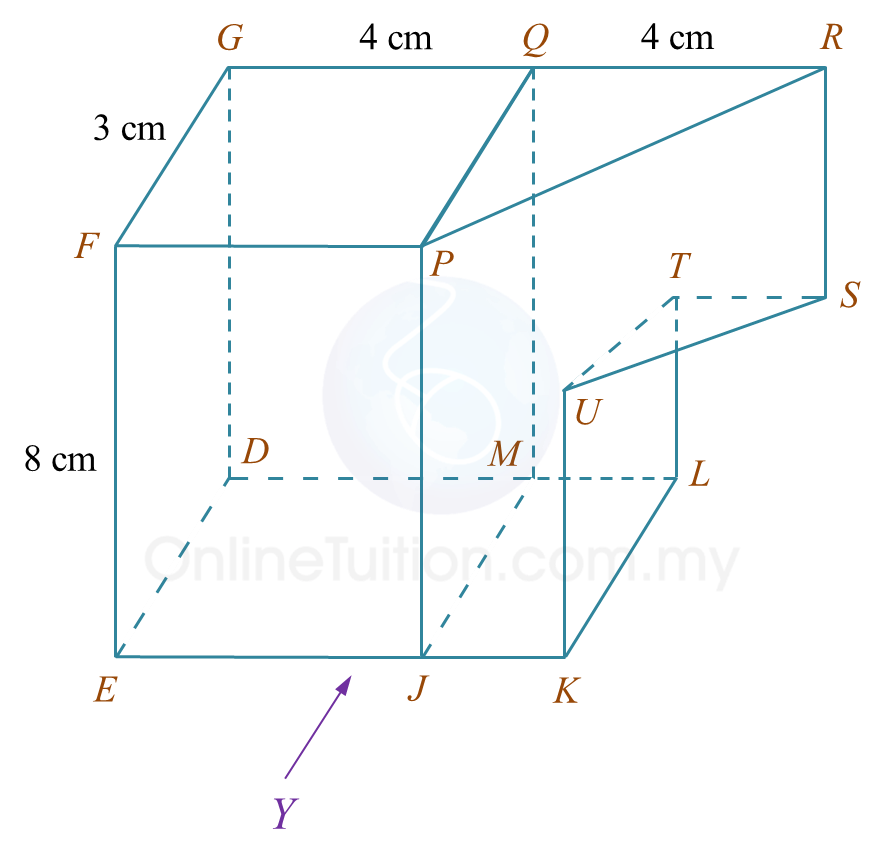Diagram 11.2
Draw to full scale,
(i) the elevation of the composite solid on a vertical plane parallel to EJK as viewed from Y.
(ii) the plan of the composite solid.
Solution:
(a)
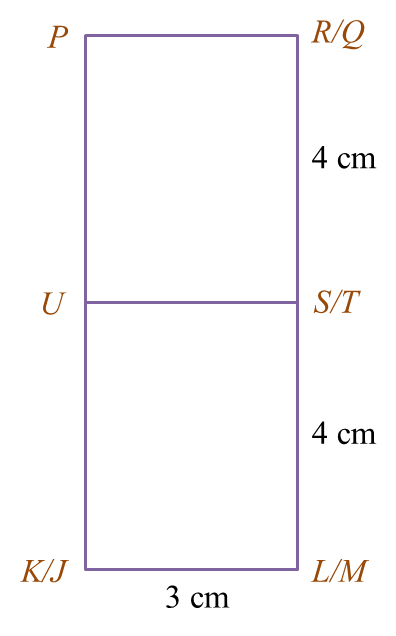
(b)(i)
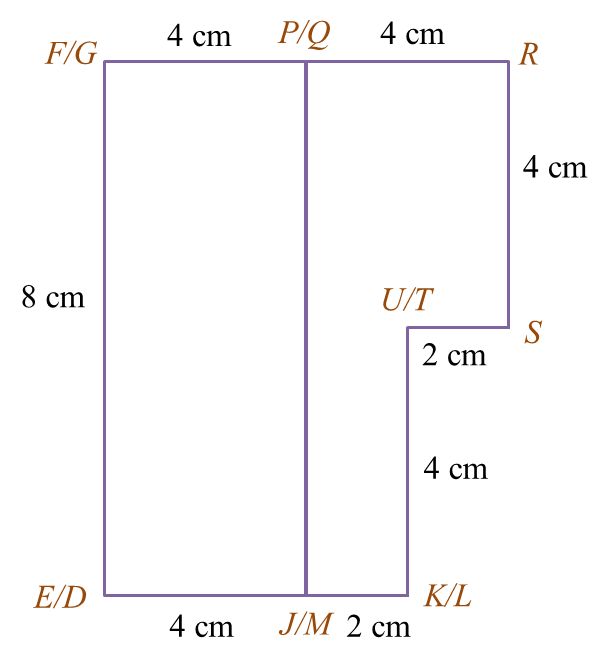
(b)(ii)
You are not allowed to use graph paper to answer this question.
(a) Diagram 11.1 shows a solid prism with a rectangular base JKLM on a horizontal plane. The surface MQRSTL is the uniform cross section of the prism. Triangle STU and PQR are horizontal planes. Edges PJ, RS and UK are vertical. PQ = TU = 3 cm.
Diagram 11.1Draw to full scale, the elevation of the solid on a vertical plane parallel to KL as viewed from X.
(b) Another solid cuboid with rectangle base JMDE is combined to the prism in Diagram 11.1 at the vertical plane JMQP. The composite solid is as shown in Diagram 11.2. The base EJKLMD lies on a horizontal plane.
Diagram 11.2Draw to full scale,
(i) the elevation of the composite solid on a vertical plane parallel to EJK as viewed from Y.
(ii) the plan of the composite solid.
Solution:
(a)
(b)(i)
(b)(ii)
Question 16 (12 marks):
Diagram 12 in the answer space shows the locations of points J, L and M, which lie on the surface of the earth. O is the centre of the earth. The longitude of M is 30o W. K is another point on the surface of the earth such that KJ is the diameter of the common parallel of latitude 45o S.
(a)(i) Mark and label point K on Diagram 12 in the answer space.
(ii) Hence, state the longitude of point K.
(b) L lies due north of M and the shortest distance from M to L measured along the surface of the earth is 7500 nautical miles.
Calculate the latitude of L.
(c) Calculate the distance, in nautical mile, from K due east to M measured along the common parallel of latitude.
(d) An aeroplane took off from K and flew due east to M along the common parallel of latitude. The average speed of the aeroplane for the flight was 750 knots.
Calculate the total time, in hour, taken for the whole flight.
Answer:
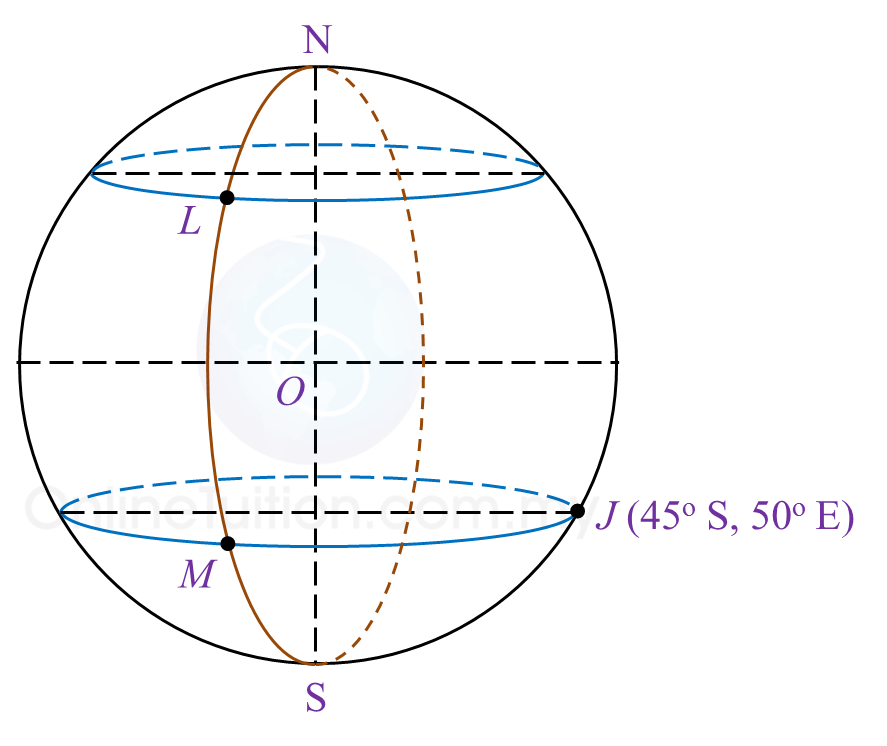
Solution:
(a)(i)
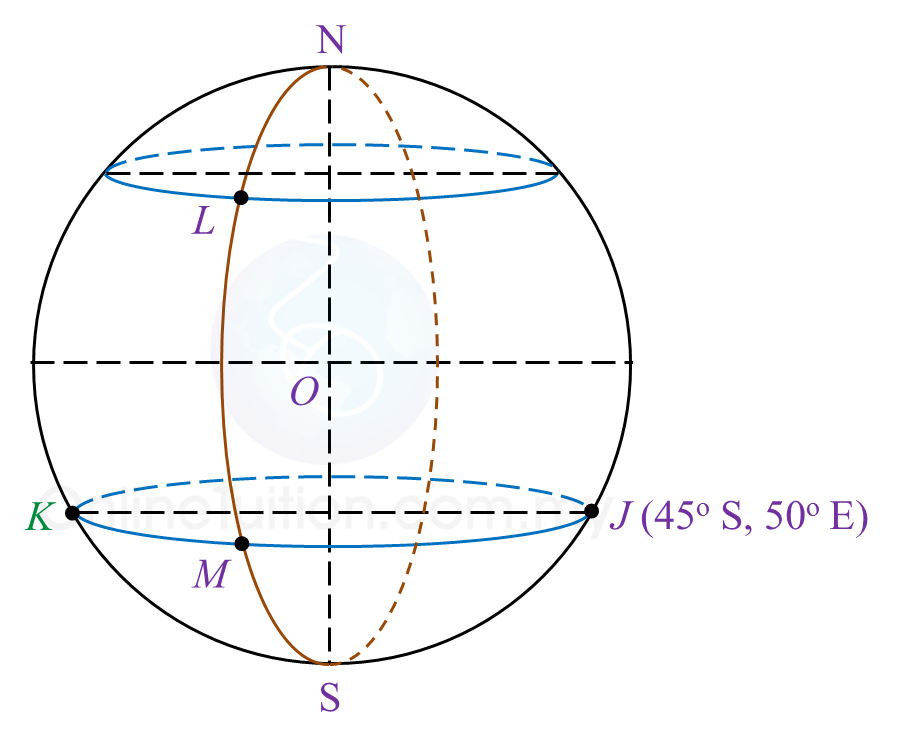
(a)(ii)
Longitude of point K = 130oW
(b)
(c)
KM = (130o – 30o) × 60 × cos 45o
= 4242.64 nautical miles
(d)
Diagram 12 in the answer space shows the locations of points J, L and M, which lie on the surface of the earth. O is the centre of the earth. The longitude of M is 30o W. K is another point on the surface of the earth such that KJ is the diameter of the common parallel of latitude 45o S.
(a)(i) Mark and label point K on Diagram 12 in the answer space.
(ii) Hence, state the longitude of point K.
(b) L lies due north of M and the shortest distance from M to L measured along the surface of the earth is 7500 nautical miles.
Calculate the latitude of L.
(c) Calculate the distance, in nautical mile, from K due east to M measured along the common parallel of latitude.
(d) An aeroplane took off from K and flew due east to M along the common parallel of latitude. The average speed of the aeroplane for the flight was 750 knots.
Calculate the total time, in hour, taken for the whole flight.
Answer:
Solution:
(a)(i)
Longitude of point K = 130oW
(b)
(c)
KM = (130o – 30o) × 60 × cos 45o
= 4242.64 nautical miles
(d)