Question 11 (6 marks):
Diagram 8 shows sectors OABC and ODE with the common centre O respectively.
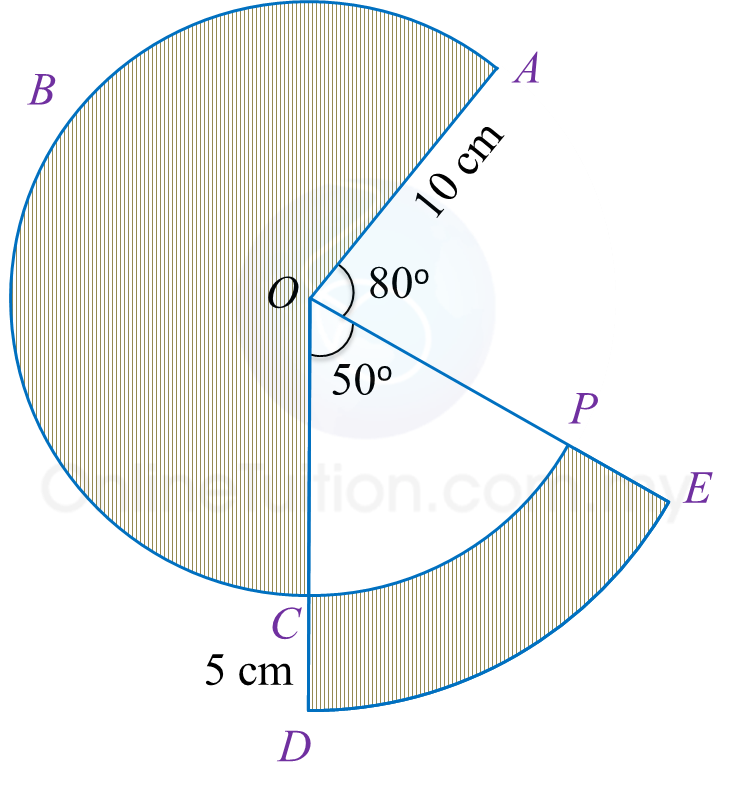 Diagram 8
Diagram 8
Calculate
(a) the perimeter, in cm, of the whole diagram,
(b) the area, in cm2, of the shaded region.
Solution:
(a)
(b)
Diagram 8 shows sectors OABC and ODE with the common centre O respectively.
 Diagram 8
Diagram 8Calculate
(a) the perimeter, in cm, of the whole diagram,
(b) the area, in cm2, of the shaded region.
Solution:
(a)
(b)
Question 12 (12 marks):
(a) Complete Table 2 in the answer space, for the equation by writing down the values of y when x = 2 and x = 5.
(b) For this part of the question, use the graph paper. You may use a flexible curve ruler.
Using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the y-axis, draw the graph of
(c) From the graph in 12(b), find
(i) the value of y when x = 2.6,
(ii) the value of x when y = 17.5.
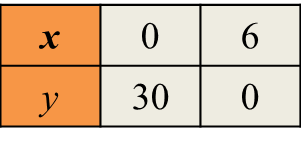
(d) Draw a suitable straight line on the graph in 12(b) to find the values of x which satisfy the equation
State the values of x.
Answer:
 Table 2
Table 2
Solution:
(a)
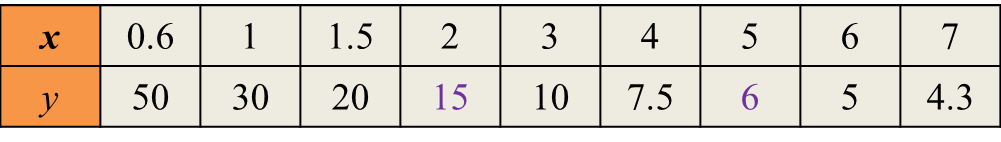
(b)
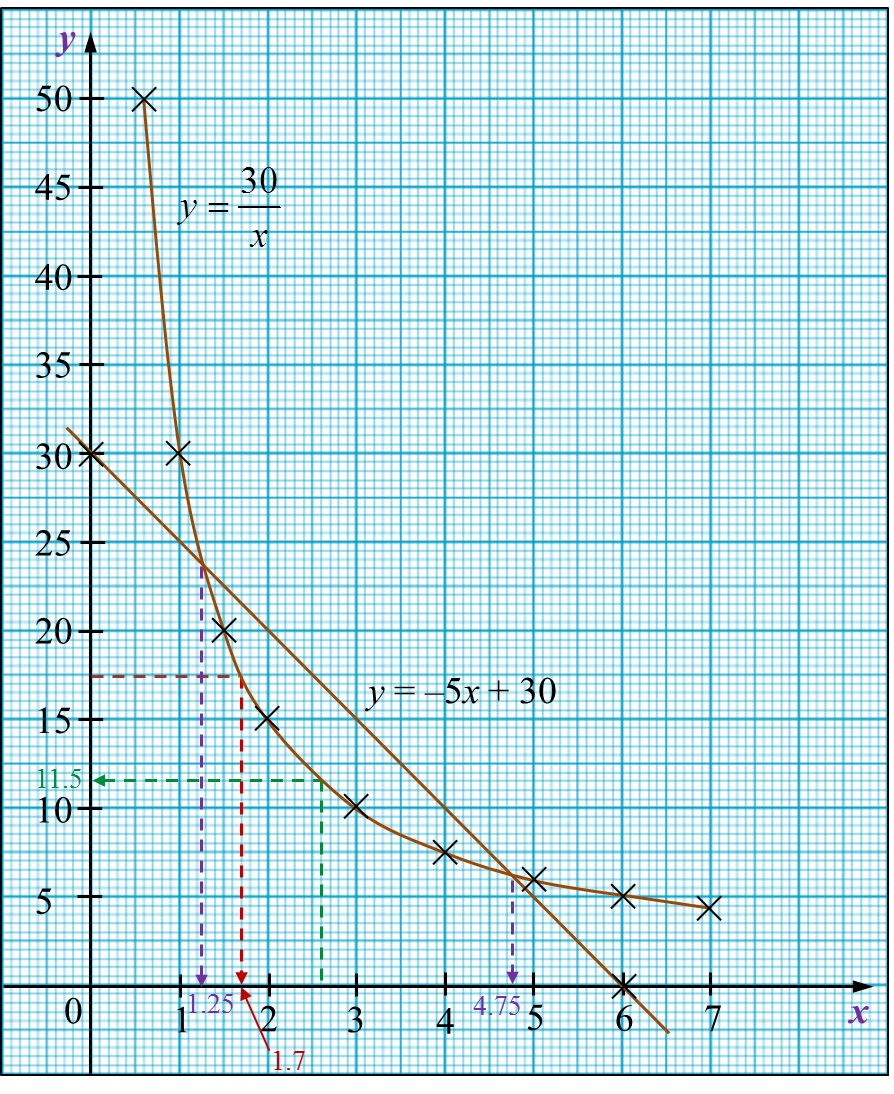
(c) From the graph
(i) When x = 2.6; y = 11.5
(ii) When y = 17.5; x = 1.7
(d)
(a) Complete Table 2 in the answer space, for the equation by writing down the values of y when x = 2 and x = 5.
(b) For this part of the question, use the graph paper. You may use a flexible curve ruler.
Using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the y-axis, draw the graph of
(c) From the graph in 12(b), find
(i) the value of y when x = 2.6,
(ii) the value of x when y = 17.5.
(d) Draw a suitable straight line on the graph in 12(b) to find the values of x which satisfy the equation
State the values of x.
Answer:
 Table 2
Table 2Solution:
(a)
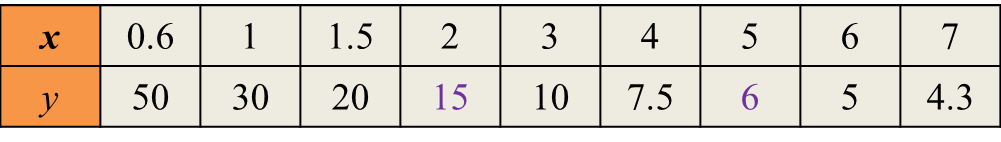
(b)

(c) From the graph
(i) When x = 2.6; y = 11.5
(ii) When y = 17.5; x = 1.7
(d)
