SPM Mathematics 2016, Paper 2 (Questions 9 & 10)

Question 9 (6 marks):
In Diagram 9, OKLM is a sector of a circle and OAB is a quadrant of a circle with common centre O.

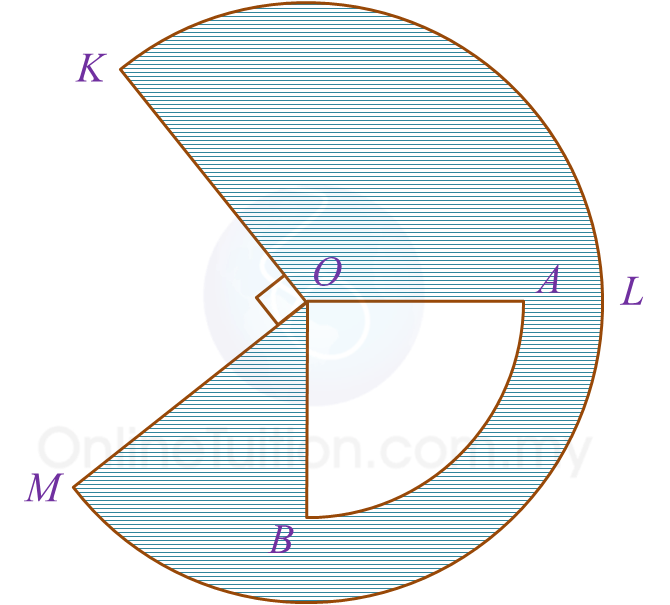Diagram 9

It is given that OA = 8 cm, ∠KOM = 90^o and OK : OB = 3 : 2.
Using $\pi =\frac{22}{7}$ , calculate
(a) the area, in cm², of the shaded region,
(b) the perimeter, in cm, of the shaded region.


Solution:
(a)
$\begin{array}{l}OB=OA=8\text{ cm and}\\ OK:OB=3:2\\ \frac{OK}{OB}=\frac{3}{2}\\ \frac{OK}{8}=\frac{3}{2}\\ OK=\frac{3}{2}\times 8\\ OK=12\\ \\ \text{Area of the shaded region}\\ =\left(\frac{{270}^o}{{360}^o}\times \frac{22}{7}\times {12}^2\right)-\left(\frac{{90}^o}{{360}^o}\times \frac{22}{7}\times 8^2\right)\\ =339\frac{3}{7}-50\frac{2}{7}\\ =289\frac{1}{7}{\text{ cm}}^2\end{array}$


(b)
$\begin{array}{l}\text{Length of arc }KLM\\ =\frac{{270}^o}{{360}^o}\times 2\times \frac{22}{7}\times 12\\ =56\frac{4}{7}\text{ cm}\\ \\ \text{Length of arc }AB\\ =\frac{{90}^o}{{360}^o}\times 2\times \frac{22}{7}\times 8\\ =12\frac{4}{7}\text{ cm}\\ \\ \text{Perimeter of shaded region}\\ =\text{Length of arc }KLM+\text{Length of }\\ \text{arc }AB+MO+OK+OA+OB\\ =56\frac{4}{7}+12\frac{4}{7}+12+12+8+8\\ =109\frac{1}{7}\text{ cm}\end{array}$

Question 10 (6 marks):
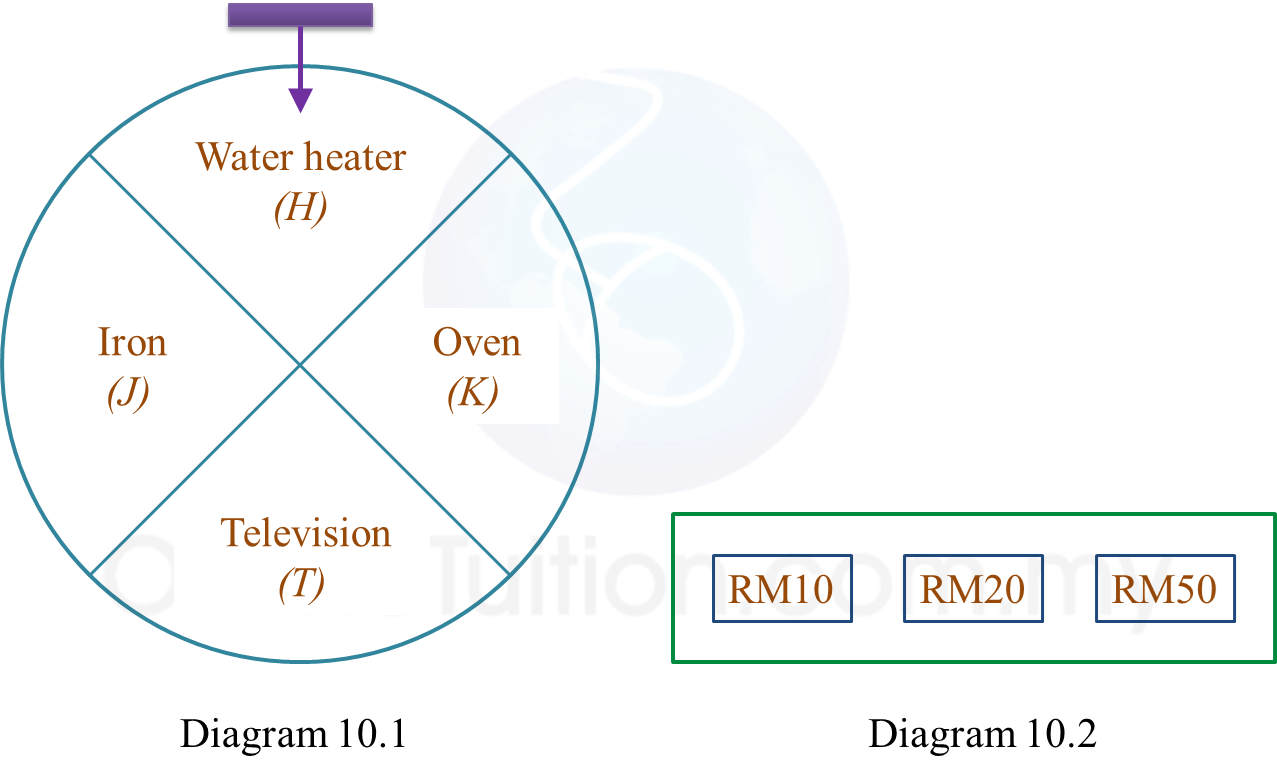
Diagram 10.1 shows a disc with four equal sectors and a fixed pointer. Each sector is labelled with water heater, oven, television and iron respectively. Diagram 10.2 shows a box which contains three cash vouchers, RM10, RM20 and RM50.



A lucky customer in a supermarket is given a chance to spin the disc once and then draw a cash voucher from the box.
(a) List the sample space for the combination of prizes that can be won.

(b) By listing down all the possible outcomes of the event, find the probability that

(i) the customer wins a television or cash voucher worth RM50,

(ii) the customer does not wins the water heater and the cash voucher worth RM20.


Solution:
(a)
S = {(Water heater, RM10), (Water heater, RM20), (Water heater, RM50), (Oven, RM10), (Oven, RM20), (Oven, RM50), (Television, RM10), (Television, RM20), (Television, RM50), (Iron, RM10), (Iron, RM20), (Iron, RM50)}

(b)(i)
{( Water heater, RM50), (Oven, RM50), (Iron, RM50), (Television, RM10), (Television, RM20), (Television, RM50)}
$\begin{array}{l}\text{Probability}\\ =\frac{6}{12}\\ =\frac{1}{2}\end{array}$

(b)(ii)
$\begin{array}{l}\text{Probability}\\ =1-P\left(\text{Water heater, RM20}\right)\\ =1-\frac{1}{12}\\ =\frac{11}{12}\end{array}$