SPM Mathematics 2016, Paper 2 (Questions 11 & 12)

Question 11 (6 marks):
Diagram 11 shows the speed-time graph for the movement of a particle for a period of t seconds.

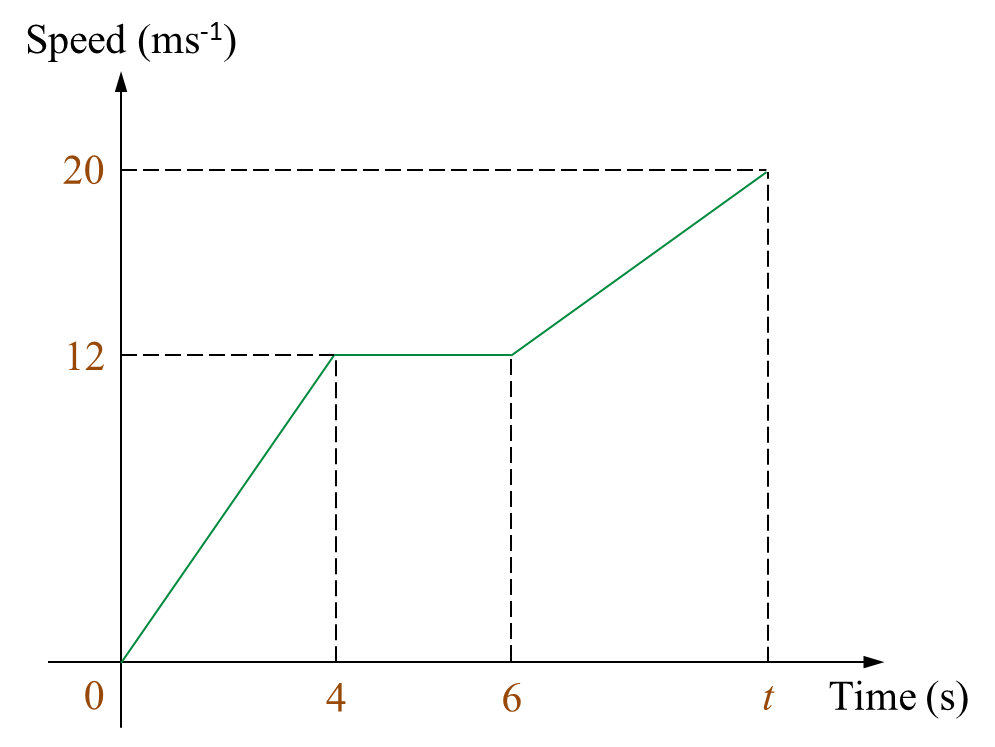Diagram 11

(a) State the uniform speed, in ms^-1, of the particle.

(b) Calculate the rate of change of speed, in ms^-2, of the particle in the first 4 seconds.

(c) Calculate the value of t, if the distance travelled in the first 4 seconds is half of the distance travelled from the 6^th second to the t^th second.


Solution:
(a)
 Uniform speed of the particle = 12 ms^-1

(b)
$\begin{array}{l}\text{Rate of change of speed of particle}\\ =\frac{12}{4}\\ =3{\text{ ms}}^{-2}\end{array}$

(c)
$\begin{array}{l}\text{Distance travelled in the first 4 seconds }\\ =\frac{1}{2}\left(\begin{array}{l}\text{Distance travelled from the }\\ {\text{6}}^{\text{th}}\text{ second to }{t}^{\text{th}}\text{ second}\end{array}\right)\\ \frac{1}{2}\times 4\times 12=\frac{1}{2}\left[\frac{1}{2}\left(12+20\right)\left(t-6\right)\right]\\ 24=\frac{1}{2}\left[16\left(t-6\right)\right]\\ 24=8\left(t-6\right)\\ 24=8t-48\\ 3=t-6\\ t=9\end{array}$

Question 12 (12 marks):
(a) Complete Table 12 in the answer space, for the equation y = –x² + 2x + 10 by writing down the values of y when x = –1 and x = 2.

(b) For this part of the question, use the graph paper. You may use a flexible curve ruler.
Using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 2 units on the y-axis, draw the graph of y = –x² + 2x + 10 for –3.5 ≤ x ≤ 4.

(c) From the graph in 12(b), find
(i) the value of y when x = –1.5,
(ii) the positive value of x when y = 8.2.


(d) Draw a suitable straight line on the graph in 12(b) to find the values of x which satisfy the equation 7 – x = x² for –3.5 ≤ x ≤ 4.
State the values of x.

Answer:



Solution:
(a)
y = –x² + 2x + 10
When x = –1
y = –(–1)² + 2(–1) + 10
y = –1 – 2 + 10
y = 7

when x = 2
y = –(2)² + 2(2) + 10
y = –4 + 4 + 10
y = 10

(b)



(c) From graph
(i) When x = –1.5; y = 4.6
(ii) When y = 8.2; x = 2.7

(d)
y = –x² + 2x + 10 ……. (1)
0 = –x² – x + 7 ………. (2)
(1) – (2): y = 3x + 3 



From graph, the values of x are –3.2 and 2.2.