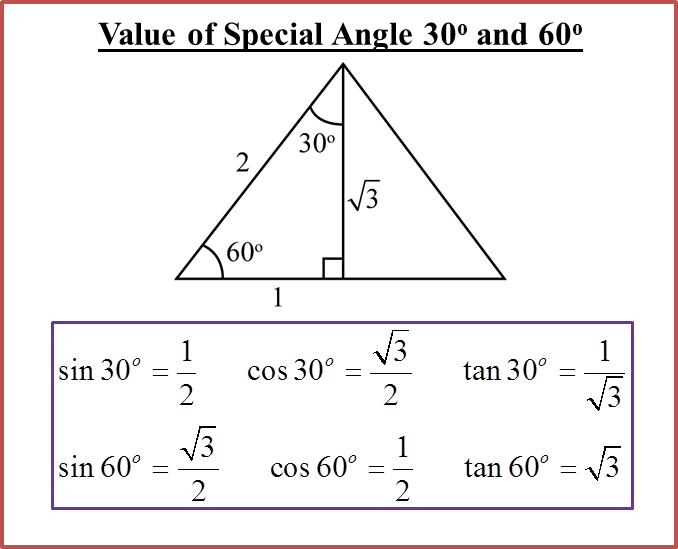
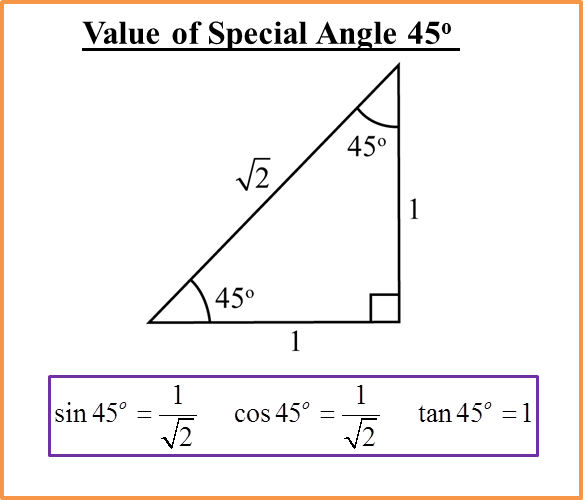
6.1.2 Values of Sine, Cosine and Tangent of an Angle (Part 2)

(A) Special Angle

(B) Finding the Angles between 0^oand 360^o Given Values of sin θ, cos θ or tan θ

1. If the value of sin θ, cos θ or tan θ is given and 0^o< θ < 360^o, the value of θ can be found using the following steps.

(a) Find the basic angle in first quadrant which corresponds to θ.

(b) Based on the sign of the value of sin θ, cos θ or tan θ, determine the quadrants in which θ lies.

(c) Find the values of θ in the right quadrants found in (b).

Example:

For each of the following cases, find the value of θ.

(a) sin θ = 0.6025 and 90^o< θ < 180^o

(b) cos θ = –0.6025 and 180^o< θ < 270^o

(c) sin θ = –0.8387 and 0^o< θ < 360^o

(d) tan θ = –1.732 and 0^o< θ < 360^o

Solution:

(a)

sin θ = 0.6025

Basic ∠ = 37.05^o ← (Press SHIFT sin^-1 0.6025 =Display: 37.04976)
∴ θ = 180^o – 37.05^o= 142.95^o ← (90^o< θ < 180^o)

(b)

cos θ = –0.6025

Basis ∠ = 52.95^o ← (Press SHIFT cos^-1 0.6025 = Display: 52.9508)

∴ θ = 180^o + 52.95^o= 232.95^o ← (180^o< θ < 270^o)

(c)

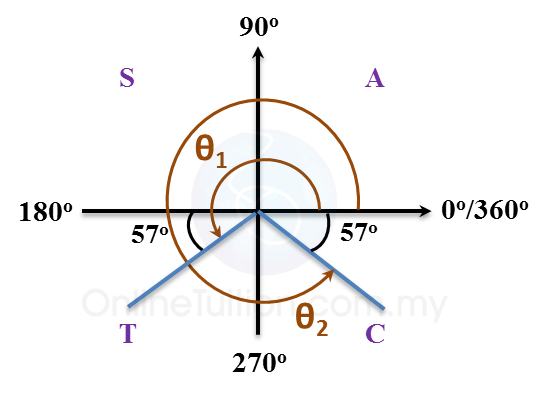
sin θ = –0.8387 ← (sin θ is negative in 3^rd quadrant and 4^thquadrant)

Basis ∠ = 57^o ← (Press SHIFT sin^-1 0.8387 = Display: 57.003)

θ₁ = 180^o + 57^o = 237^o ← (180^o< θ < 270^o)

θ₂ = 360^o – 57^o = 303^o ← (270^o< θ < 360^o)

∴ θ = 237^oand 303^o

(d)

tan θ = –1.732 ← (tan θ is negative in 2^nd quadrant and 4^thquadrant)

Basis ∠ = 60^o ← (Press SHIFT tan^-1 1.732 = Display: 59.9993)

θ₁ = 180^o – 60^o = 120^o ← (90^o< θ < 180^o)

θ₂ = 360^o – 60^o = 300^o ← (270^o< θ < 360^o)
∴ θ = 120^oand 300^o