6.1.1 Values of Sine, Cosine and Tangent of an Angle (Part 1)

6.1 Values of Sine, Cosine and Tangent of an Angle

(A) Sine, Cosine and Tangent for Right-Angled Triangles

\begin{array}{l} \sin θ = \frac{opposites side}{hypotenuse} \\ cos θ = \frac{adjacent side}{hypotenuse} \\ tan θ = \frac{opposites side}{adjacent side} \end{array}

(B) Values of Sin θ, Cos θ and Tan θ in First Quadrant of the Unit Circle

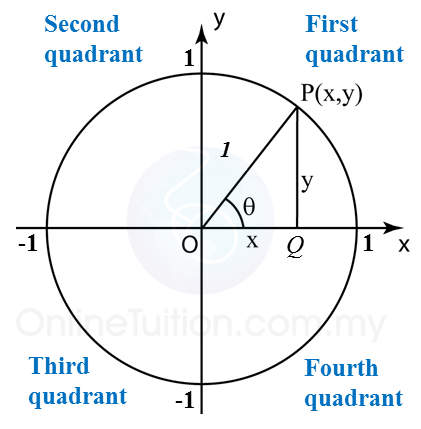
In first quadrant, P is a point on the circumference of the unit circle with centre O, θ is the angle between the radius OP and the positive x-axis. From the diagram,

\begin{array}{l} (a) sin θ = \frac{P Q}{O P} = y \\ (b) cos θ = \frac{O Q}{O P} = x \\ (c) tan θ = \frac{P Q}{O Q} = \frac{y}{x} \\ T h e r e f o r e, \\ \begin{array}{l} sin θ = y -coordinate \\ cos θ = x -coordinate \\ tan θ = \frac{y -coordinate}{x -coordinate} \end{array} \end{array}

(C) A Cartesian plane is divided into four parts called quadrants by the x-axis and the y-axis. The quadrants are named as first quadrant, second quadrant, third quadrant and fourth quadrant in the anticlockwise direction.

Quick recall:

All – Add

Sine – Sugar

Tangent – To

Cosine – Coffee

Example:

Determine whether the value of each of the following is positive or negative.

(a) sin 105^o (b) cos 75^o (c) tan 305^o (d) sin 50^o

(e) cos 160^o (f) tan 220^o (g) cos 260^o (h) cos 350^o

Solution:

(a) sin 105^o is positive because 90^o< 105^o< 180^o (in second quadrant).

(b) cos 75^o is positive because 0^o< 75^o< 90^o (in first quadrant).

(c) tan 305^o is negative because 270^o< 305^o< 360^o (in fourth quadrant).

(d) sin 50^o is positive because 0^o< 50^o< 90^o (in first quadrant).

(e) cos 160^o is negative because 90^o< 160^o< 180^o (in second quadrant).

(f) tan 220^o is positive because 180^o< 220^o< 270^o (in third quadrant).

(g) cos 260^o is negative because 180^o< 260^o< 270^o (in third quadrant).

(h) cos 350^o is positive because 270^o< 350^o< 360^o (in fourth quadrant).

Leave a Comment Cancel reply