Question 15 (12 marks):
You are not allowed to use graph paper to answer this question.
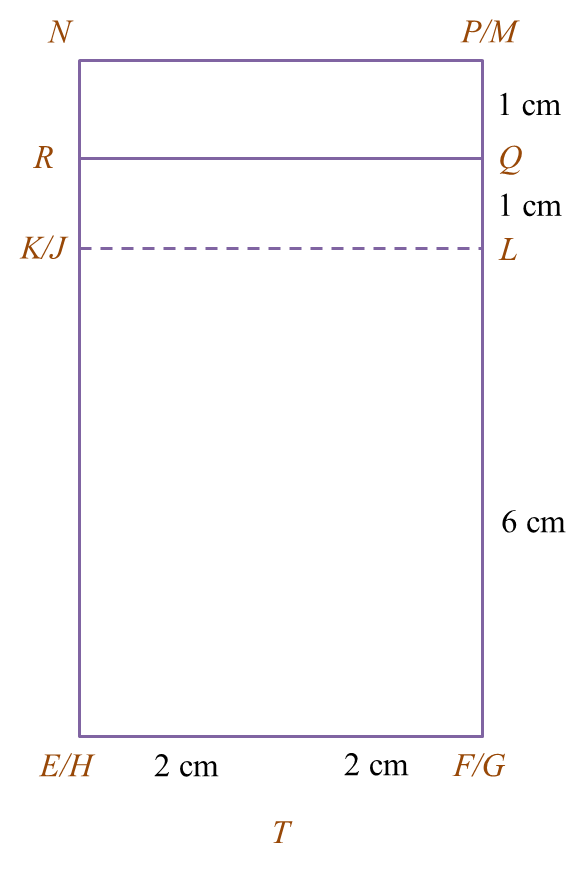
(a) Diagram 9.1 shows two solid right prisms joined at the vertical plane EGLK. The planes JKL and MNP are the uniform cross sections of the prism HEGLJK and prism EFGMNP respectively. The base EFGH is a rectangle which lies on a horizontal plane. Edges HJ and EK are vertical.
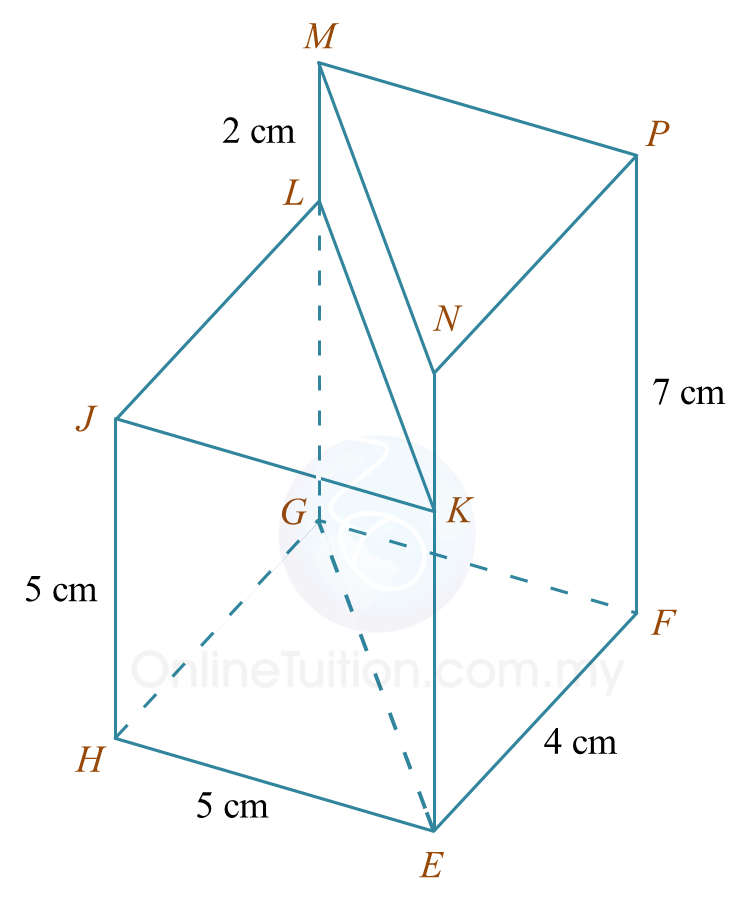 Diagram 9.1
Diagram 9.1
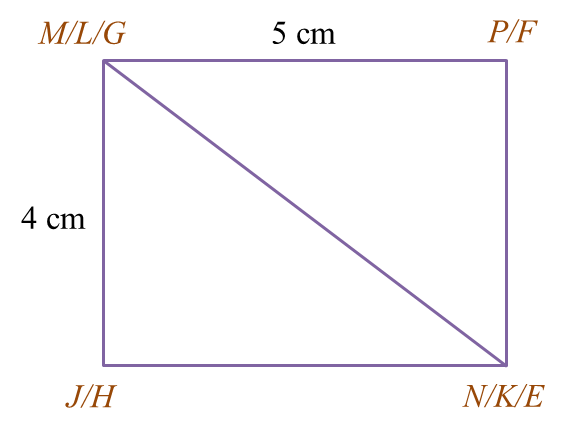
Draw, to full scale, the plan of the composite solid.
(b) Another solid half cylinder with a diameter of 4 cm is joined to the prism in Diagram 9.1 at the vertical plane EFQR. The composite solid is as shown in Diagram 9.2. The base HETFG lies on a horizontal plane.
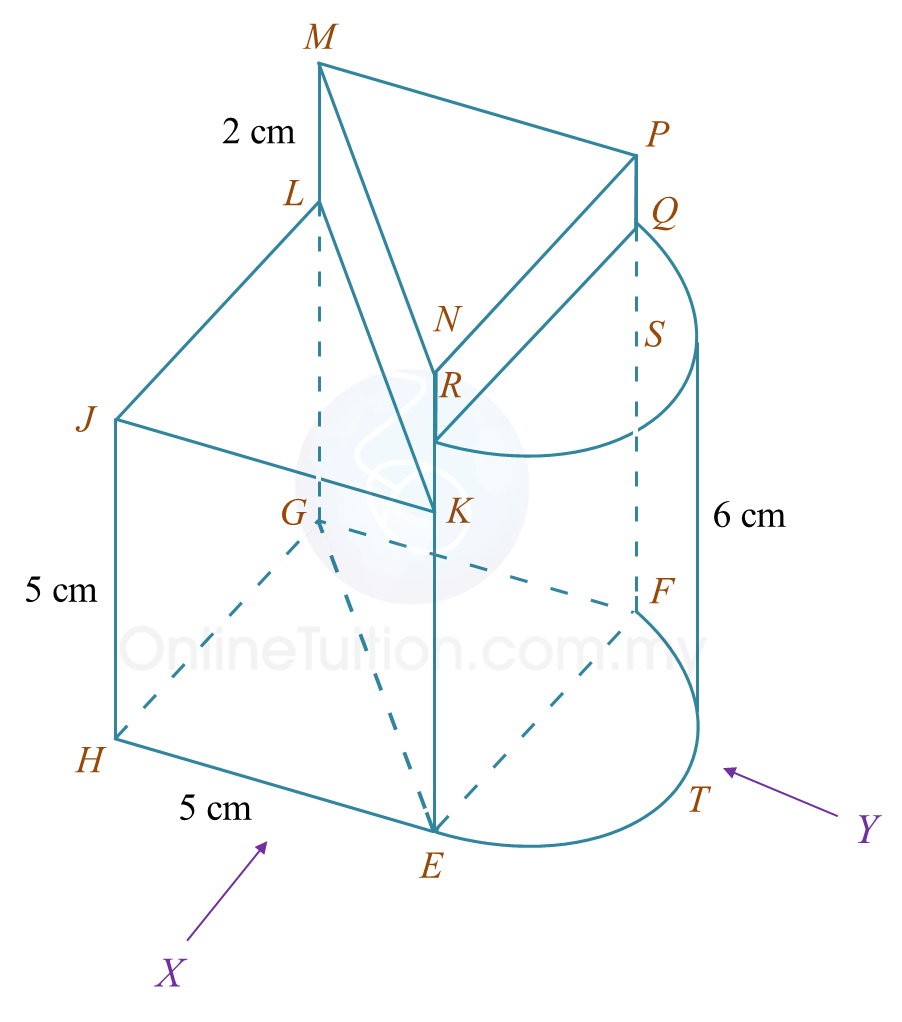 Diagram 9.2
Diagram 9.2
Draw to full scale,
(i) the elevation of the composite solid on a vertical plane parallel to HE as viewed from X.
(ii) the elevation of the composite solid on a vertical plane parallel to EF as viewed from Y.
Solution:
(a)
(b)(i)
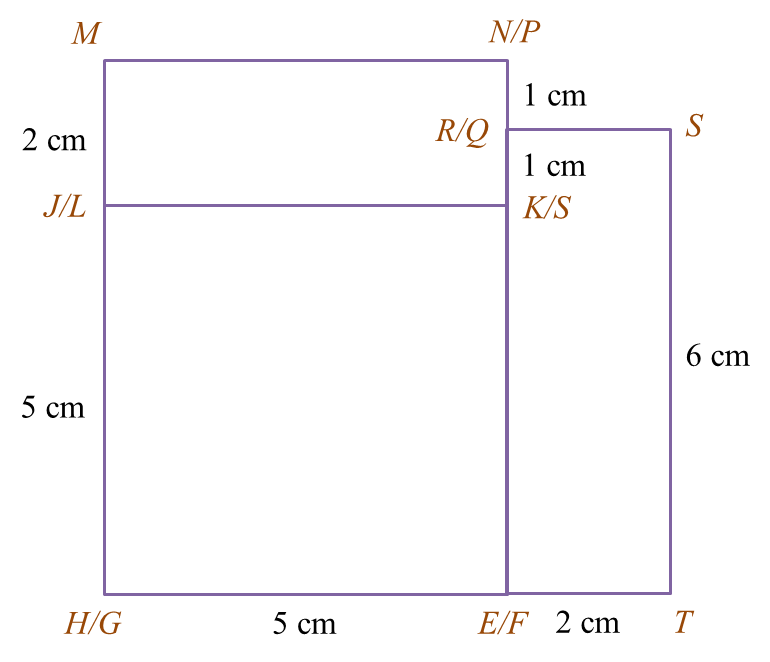
(b)(ii)
You are not allowed to use graph paper to answer this question.
(a) Diagram 9.1 shows two solid right prisms joined at the vertical plane EGLK. The planes JKL and MNP are the uniform cross sections of the prism HEGLJK and prism EFGMNP respectively. The base EFGH is a rectangle which lies on a horizontal plane. Edges HJ and EK are vertical.
 Diagram 9.1
Diagram 9.1Draw, to full scale, the plan of the composite solid.
(b) Another solid half cylinder with a diameter of 4 cm is joined to the prism in Diagram 9.1 at the vertical plane EFQR. The composite solid is as shown in Diagram 9.2. The base HETFG lies on a horizontal plane.
 Diagram 9.2
Diagram 9.2Draw to full scale,
(i) the elevation of the composite solid on a vertical plane parallel to HE as viewed from X.
(ii) the elevation of the composite solid on a vertical plane parallel to EF as viewed from Y.
Solution:
(a)

(b)(i)

(b)(ii)

Question 16 (12 marks):
Diagram 10 shows four points, G, H, I and J on the surface of the Earth. JI is the diameter of the parallel of latitude 50o N. O is the centre of the Earth.
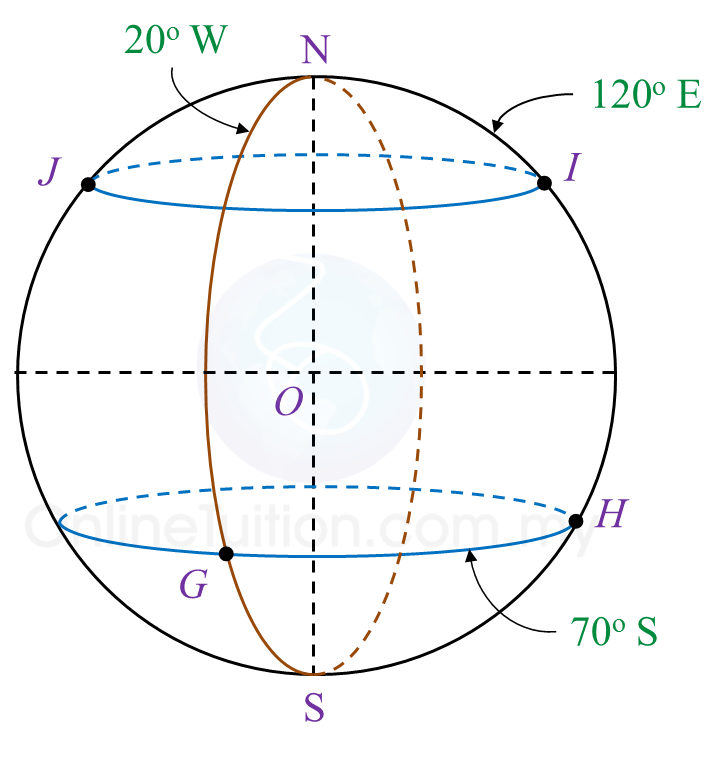 Diagram 10
Diagram 10
(a) State the location of G.
(b) Calculate the shortest distance, in nautical mile, from I to J measured along the surface of the Earth.
(c) Calculate the shortest distance, in nautical mile, from G to H measured along the common parallel of latitude.
(d) An aeroplane took off from I and flew due south to point P. The average speed of the journey was 800 knots. The time taken for the flight was 5.25 hours.
Calculate the latitude of P.
Solution:
(a)
Location of G = (70o S, 20o W)
(b)
∠ JOI
= 180o – 50o – 50o
= 80o
Distance of I to J
= 80o × 60’
= 4800 nautical miles
(c)
Distance of G to H
= (20o + 120o) × 60’ × cos 70o
= 140o × 60’ × cos 70o
= 2872.97 nautical miles
(d)
Average speed=Total distance travelledTotal time taken800=x5.25x=4200 nautical milesI to P=4200Difference between parallel=yy×60=4200y=70oThus, latitude of P=70o−50o=20oS
Diagram 10 shows four points, G, H, I and J on the surface of the Earth. JI is the diameter of the parallel of latitude 50o N. O is the centre of the Earth.
 Diagram 10
Diagram 10(a) State the location of G.
(b) Calculate the shortest distance, in nautical mile, from I to J measured along the surface of the Earth.
(c) Calculate the shortest distance, in nautical mile, from G to H measured along the common parallel of latitude.
(d) An aeroplane took off from I and flew due south to point P. The average speed of the journey was 800 knots. The time taken for the flight was 5.25 hours.
Calculate the latitude of P.
Solution:
(a)
Location of G = (70o S, 20o W)
(b)
∠ JOI
= 180o – 50o – 50o
= 80o
Distance of I to J
= 80o × 60’
= 4800 nautical miles
Distance of G to H
= (20o + 120o) × 60’ × cos 70o
= 140o × 60’ × cos 70o
= 2872.97 nautical miles
(d)
Average speed=Total distance travelledTotal time taken800=x5.25x=4200 nautical milesI to P=4200Difference between parallel=yy×60=4200y=70oThus, latitude of P=70o−50o=20oS