Question 11 (6 marks):
Diagram 6 shows the distance-time graph of Ursula, Janet and Maria in a 100 m race.
 Diagram 6
Diagram 6

(a) Who won the race?
(b) During the race, Ursula slipped and fell over. After that, she continued her run.
State the duration, in seconds, before Ursula continued her run.
(c) During the race, Janet was injured and she stopped running.
State Janet’s distance, in m, from the finishing line when she stopped running.
(d) Calculate the average speed, in ms-1, of Ursula.
Solution:
(a)
Maria won the race: 100 km in 16 seconds.
(b)
Duration before Ursula continued her run from slipping and falling over
= 18 seconds – 9 seconds
= 9 seconds
(c)
Janet’s distance from the finishing line when she stopped running
= 100 m – 70 m
= 30 m
(d)
Diagram 6 shows the distance-time graph of Ursula, Janet and Maria in a 100 m race.
 Diagram 6
Diagram 6
(a) Who won the race?
(b) During the race, Ursula slipped and fell over. After that, she continued her run.
State the duration, in seconds, before Ursula continued her run.
(c) During the race, Janet was injured and she stopped running.
State Janet’s distance, in m, from the finishing line when she stopped running.
(d) Calculate the average speed, in ms-1, of Ursula.
Solution:
(a)
Maria won the race: 100 km in 16 seconds.
(b)
Duration before Ursula continued her run from slipping and falling over
= 18 seconds – 9 seconds
= 9 seconds
(c)
Janet’s distance from the finishing line when she stopped running
= 100 m – 70 m
= 30 m
(d)
Question 12 (12 marks):
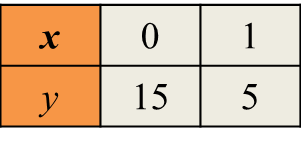
(a) Complete Table 2 in the answer space, for the equation y = –x3 + 4x + 10 by writing down the values of y when x = –2 and x = 1.5.
(b) For this part of the question, use the graph paper. You may use a flexible curve ruler.
Using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 10 units on the y-axis, draw the graph of y = –x3 + 4x + 10 for –3 ≤ x ≤ 4.
(c) From the graph in 12(b), find
(i) the value of y when x = –2.5,
(ii) the positive value of x when y = 4.
(d) Draw a suitable straight line on the graph in 12(b) to find the values of x which satisfy the equation x3 – 14x + 5 = 0 for –3 ≤ x ≤ 4.
State the values of x.
Answer:

Solution:
(a)
y = –x3 + 4x + 10
When x = –2
y = –(–2)3 + 4(–2) + 10
y = 8 – 8 + 10
y = 10
When x = 1.5
y = –(1.5)3 + 4(1.5) + 10
y = –3.375 + 6 + 10
y = 12.625
(b)
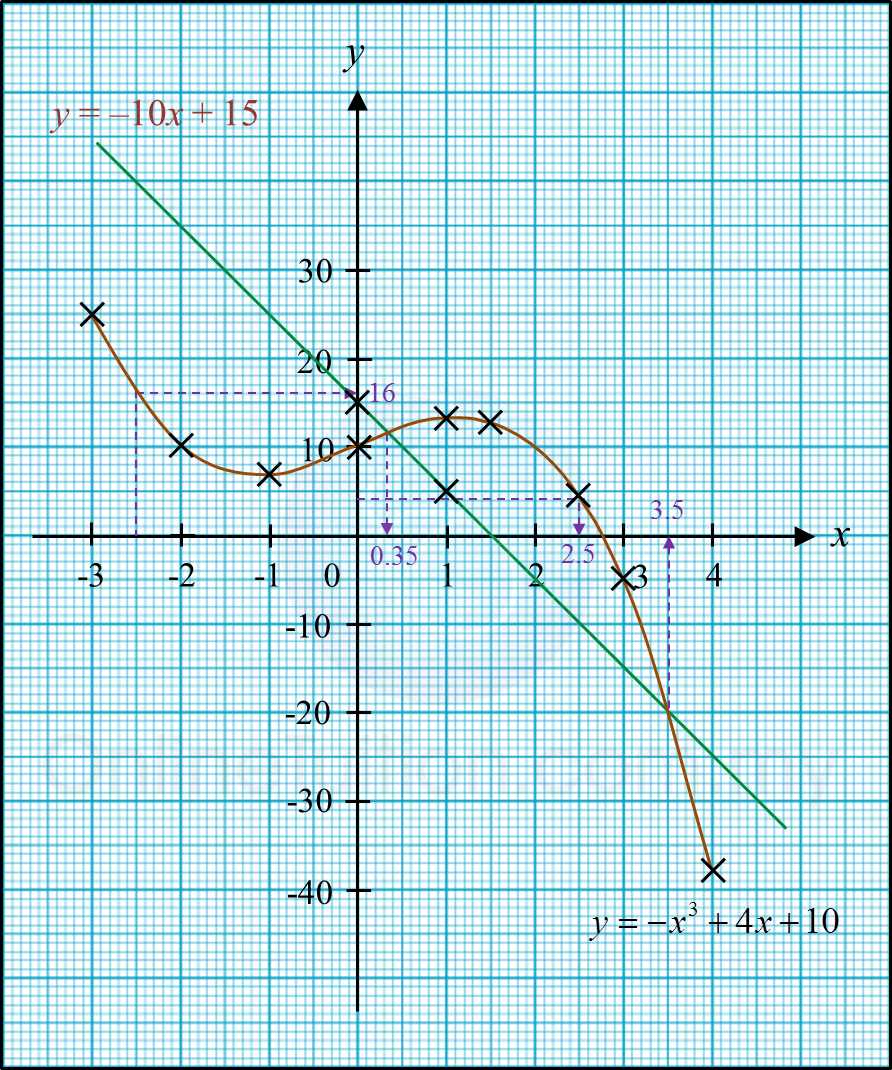
(c) From graph
(i) When x = –2.5; y = 16
(ii) When y = 4; x = 2.5
(d)
x3 – 14x + 5 = 0
–x3 + 14x – 5 = 0
–x3 + (4x + 10x) + (10 – 15) = 0
–x3 + 4x + 10 = –10x + 15
Thus, y = –10x + 15
From graph, the values of x are 0.35 and 3.5.
(a) Complete Table 2 in the answer space, for the equation y = –x3 + 4x + 10 by writing down the values of y when x = –2 and x = 1.5.
(b) For this part of the question, use the graph paper. You may use a flexible curve ruler.
Using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 10 units on the y-axis, draw the graph of y = –x3 + 4x + 10 for –3 ≤ x ≤ 4.
(c) From the graph in 12(b), find
(i) the value of y when x = –2.5,
(ii) the positive value of x when y = 4.
(d) Draw a suitable straight line on the graph in 12(b) to find the values of x which satisfy the equation x3 – 14x + 5 = 0 for –3 ≤ x ≤ 4.
State the values of x.
Answer:

Solution:
(a)
y = –x3 + 4x + 10
When x = –2
y = –(–2)3 + 4(–2) + 10
y = 8 – 8 + 10
y = 10
When x = 1.5
y = –(1.5)3 + 4(1.5) + 10
y = –3.375 + 6 + 10
y = 12.625
(b)

(c) From graph
(i) When x = –2.5; y = 16
(ii) When y = 4; x = 2.5
(d)
x3 – 14x + 5 = 0
–x3 + 14x – 5 = 0
–x3 + (4x + 10x) + (10 – 15) = 0
–x3 + 4x + 10 = –10x + 15
Thus, y = –10x + 15

From graph, the values of x are 0.35 and 3.5.