SPM Mathematics Trial 2024 (Selangor Set 2), Paper 2 (Question 14)

Question 14:
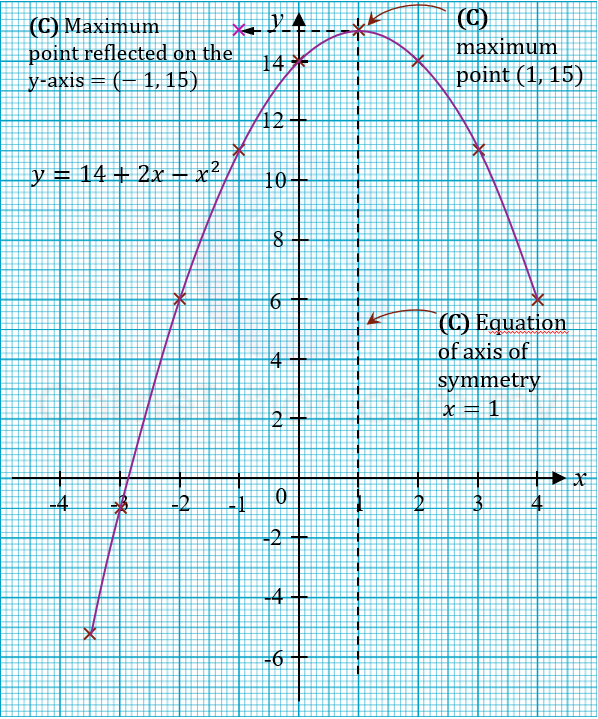
(a) Complete Table 4 in the answer space for the equation y = 14 + 2x – x² by writing down the values of y when x = -2 and x = 1. [2 marks]

(b) For this part of question, use the graph paper provided on page 27. You may use a flexible curve rule.

By using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 2 units on the y-axis, draw the graph of y = 14 + 2x – x² for -3.5 ≤ x ≤ 4. [4 marks]

(c) Determine the equation of axis of symmetry and the coordinate of maximum point when the graph in 14(b) is reflected on the y-axis. [2 marks]

Answer:

Solution:
(a)
$$\begin{aligned} & y=14+2 x-x^2 \\ & \text { When } x=-2 \\ & y=14+2(-2)-(-2)^2 \\ & y=14-4-4 \\ & y=6 \end{aligned}$$
$$\begin{aligned} &\text { When } x=1\\ &\begin{aligned} & y=14+2(1)-(1)^2 \\ & y=14+2-1 \\ & y=15 \end{aligned} \end{aligned}$$


(b)(c)