Question 17(a):
Water rocket competition is getting popular among students in Malaysia.
(a) Diagram 12 shows the path of the water rocket recorded using a stroboscope when it is launched on vertical plane that is drawn on a Cartesian plane.
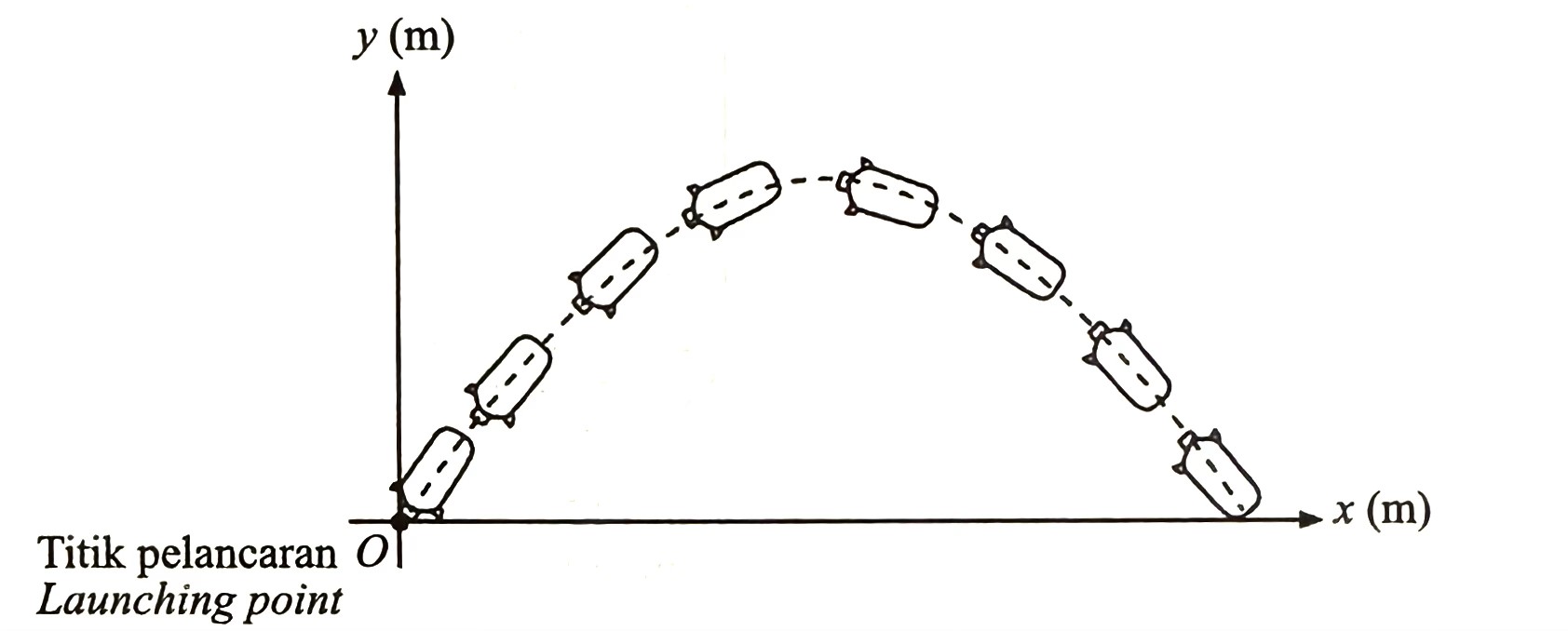
(i) The path of the water rocket is represented by the quadratic function, f(x)=ax2 + bx + c. State the range of the value of a. [1 mark]
(ii) The water rocket reaches a maximum height of 5 m from the ground and landed 8 m from the launching point. State the coordinates of the maximum point of the water rocket’s path. [2 marks]
Solution:
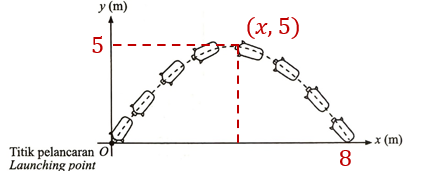
(a)(i) Range of the value is, a < 0
(a)(ii)
$$ \begin{aligned} &\begin{aligned} x & =\frac{0+8}{2} \\ & =4 \end{aligned}\\ &\text { Coordinates of the maximum point }=(4,5) \end{aligned} $$
Water rocket competition is getting popular among students in Malaysia.
(a) Diagram 12 shows the path of the water rocket recorded using a stroboscope when it is launched on vertical plane that is drawn on a Cartesian plane.

(i) The path of the water rocket is represented by the quadratic function, f(x)=ax2 + bx + c. State the range of the value of a. [1 mark]
(ii) The water rocket reaches a maximum height of 5 m from the ground and landed 8 m from the launching point. State the coordinates of the maximum point of the water rocket’s path. [2 marks]
Solution:

(a)(i) Range of the value is, a < 0
(a)(ii)
$$ \begin{aligned} &\begin{aligned} x & =\frac{0+8}{2} \\ & =4 \end{aligned}\\ &\text { Coordinates of the maximum point }=(4,5) \end{aligned} $$
Question 17(b):
(b) Table 11 shows the estimated production cost for a unit of water rocket for several teams which competed in a STEM carnival.

Calculate the standard deviation of the data. [3 marks]
Solution:
$$ \text { Midpoint }, x \text { of the estimated cost }=\frac{15+19}{2}=17 $$

$$ \begin{aligned} \operatorname{Mean}, \bar{x}=\frac{\sum f x}{\Sigma f} & =\frac{5(17)+3(22)+6(27)+2(32)}{5+3+6+2} \\ & =\frac{377}{16} \\ & =23.56 \end{aligned} $$
$$ \begin{aligned} &\text { Standard deviation, } \sigma=\sqrt{\frac{\Sigma f x^2}{\Sigma f}-\bar{x}^2}\\ &\begin{aligned} & =\sqrt{\frac{5(17)^2+3(22)^2+6(27)^2+2(32)^2}{16}-23.56^2} \\ & =\sqrt{\frac{9319}{16}-23.56^2} \\ & =5.23 \end{aligned} \end{aligned} $$
(b) Table 11 shows the estimated production cost for a unit of water rocket for several teams which competed in a STEM carnival.

Calculate the standard deviation of the data. [3 marks]
Solution:
$$ \text { Midpoint }, x \text { of the estimated cost }=\frac{15+19}{2}=17 $$

$$ \begin{aligned} \operatorname{Mean}, \bar{x}=\frac{\sum f x}{\Sigma f} & =\frac{5(17)+3(22)+6(27)+2(32)}{5+3+6+2} \\ & =\frac{377}{16} \\ & =23.56 \end{aligned} $$
$$ \begin{aligned} &\text { Standard deviation, } \sigma=\sqrt{\frac{\Sigma f x^2}{\Sigma f}-\bar{x}^2}\\ &\begin{aligned} & =\sqrt{\frac{5(17)^2+3(22)^2+6(27)^2+2(32)^2}{16}-23.56^2} \\ & =\sqrt{\frac{9319}{16}-23.56^2} \\ & =5.23 \end{aligned} \end{aligned} $$
Question 17(c):
(c) Diagram 13 shows the design of the water rocket bottle which consists of the combination of a hemisphere, a cylinder and a cone. It is given that all the three shapes have the same radius. The height of the cylinder is four times its radius and the height of the cone is the same as its radius.
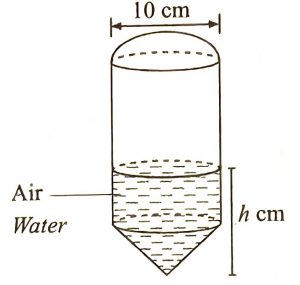
If 1/3 of the volume of the bottle is filled with water, calculate the value of h.
[5 marks]
(use π = 22/7 )
Solution:
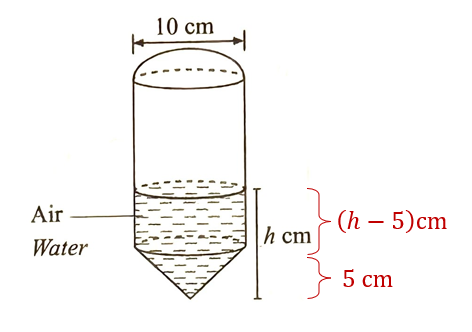 $$
\text { Radius }=\frac{10}{2}=5 \mathrm{~cm}
$$
$$
\text { Radius }=\frac{10}{2}=5 \mathrm{~cm}
$$
$$ \begin{aligned} &\text { Volume of hemisphere, }\\ &\begin{aligned} V_1 & =\frac{2}{3} \pi r^3 \\ & =\frac{2}{3} \times \frac{22}{7} \times 5^3 \\ & =\frac{5500}{21} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Volume of cylinder, } V_2=\pi r^2 h_2\\ &\begin{aligned} & =\frac{22}{7} \times 5^2 \times(4 \times 5) \\ & =\frac{11000}{7} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Volume of cone, }\\ &\begin{aligned} V_3 & =\frac{1}{3} \pi r^2 h_3 \\ & =\frac{1}{3} \times \frac{22}{7} \times 5^2 \times 5 \\ & =\frac{2750}{21} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Volume of water } & =\frac{1}{3}\left(\frac{5500}{21}+\frac{11000}{7}+\frac{2750}{21}\right) \\ & =\frac{13750}{21} \mathrm{~cm}^3 \end{aligned} $$
$$ \text { Volume of water }=\text { volume of cylinder that filled with water }+ \text { volume of cone, } V_3 $$
$$ \begin{aligned} \frac{22}{7} \times 5^2 \times(h-5)+\frac{2750}{21} & =\frac{13750}{21} \\ \frac{550}{7} \times(h-5) & =\frac{13750}{21}-\frac{2750}{21} \\ h-5 & =\frac{11000}{21} \times \frac{7}{550} \\ h-5 & =\frac{20}{3} \\ & =11 \frac{2}{3} \mathrm{~cm} \end{aligned} $$
(c) Diagram 13 shows the design of the water rocket bottle which consists of the combination of a hemisphere, a cylinder and a cone. It is given that all the three shapes have the same radius. The height of the cylinder is four times its radius and the height of the cone is the same as its radius.

If 1/3 of the volume of the bottle is filled with water, calculate the value of h.
[5 marks]
(use π = 22/7 )
Solution:
 $$
\text { Radius }=\frac{10}{2}=5 \mathrm{~cm}
$$
$$
\text { Radius }=\frac{10}{2}=5 \mathrm{~cm}
$$$$ \begin{aligned} &\text { Volume of hemisphere, }\\ &\begin{aligned} V_1 & =\frac{2}{3} \pi r^3 \\ & =\frac{2}{3} \times \frac{22}{7} \times 5^3 \\ & =\frac{5500}{21} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Volume of cylinder, } V_2=\pi r^2 h_2\\ &\begin{aligned} & =\frac{22}{7} \times 5^2 \times(4 \times 5) \\ & =\frac{11000}{7} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Volume of cone, }\\ &\begin{aligned} V_3 & =\frac{1}{3} \pi r^2 h_3 \\ & =\frac{1}{3} \times \frac{22}{7} \times 5^2 \times 5 \\ & =\frac{2750}{21} \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Volume of water } & =\frac{1}{3}\left(\frac{5500}{21}+\frac{11000}{7}+\frac{2750}{21}\right) \\ & =\frac{13750}{21} \mathrm{~cm}^3 \end{aligned} $$
$$ \text { Volume of water }=\text { volume of cylinder that filled with water }+ \text { volume of cone, } V_3 $$
$$ \begin{aligned} \frac{22}{7} \times 5^2 \times(h-5)+\frac{2750}{21} & =\frac{13750}{21} \\ \frac{550}{7} \times(h-5) & =\frac{13750}{21}-\frac{2750}{21} \\ h-5 & =\frac{11000}{21} \times \frac{7}{550} \\ h-5 & =\frac{20}{3} \\ & =11 \frac{2}{3} \mathrm{~cm} \end{aligned} $$
Question 17(d):
The relationship between the launching angle of the water rocket, θ and the landing distance, l is represented by a trigonometric formulae $$ l=\frac{u^2}{g}(2 \sin \theta \operatorname{cos} \theta) $$ where u is the initial velocity of the water rocket and g is the gravitational acceleration.
A student wants to determine either 30∘ or 45∘ as the launching angle of his water rocket so that the water rocket will land further. It is given that u = 20 ms-1 and g = 10 ms-2.
Without using a calculator, determine is the best launching angle for the water rocket. [4 marks]
Solution:
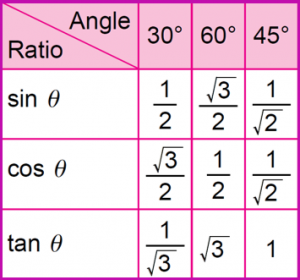
$$ l=\frac{u^2}{g}(2 \sin \theta \operatorname{cos} \theta) $$
$$ \begin{aligned} l_{30^{\circ}} & =\frac{20^2}{10}\left(2 \sin 30^{\circ} \mathrm{cos} 30^{\circ}\right) \\ & =40\left(2 \times \frac{1}{2} \times \frac{\sqrt{3}}{2}\right) \\ & =20 \sqrt{3} \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} l_{45^{\circ}} & =\frac{20^2}{10}\left(2 \sin 45^{\circ} \operatorname{cos} 45^{\circ}\right) \\ & =40\left(2 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}\right) \\ & =40 \mathrm{~m} \end{aligned} $$
$$ \therefore \text { The best launching angle is } 45^{\circ} \text {. } $$
The relationship between the launching angle of the water rocket, θ and the landing distance, l is represented by a trigonometric formulae $$ l=\frac{u^2}{g}(2 \sin \theta \operatorname{cos} \theta) $$ where u is the initial velocity of the water rocket and g is the gravitational acceleration.
A student wants to determine either 30∘ or 45∘ as the launching angle of his water rocket so that the water rocket will land further. It is given that u = 20 ms-1 and g = 10 ms-2.
Without using a calculator, determine is the best launching angle for the water rocket. [4 marks]
Solution:

$$ l=\frac{u^2}{g}(2 \sin \theta \operatorname{cos} \theta) $$
$$ \begin{aligned} l_{30^{\circ}} & =\frac{20^2}{10}\left(2 \sin 30^{\circ} \mathrm{cos} 30^{\circ}\right) \\ & =40\left(2 \times \frac{1}{2} \times \frac{\sqrt{3}}{2}\right) \\ & =20 \sqrt{3} \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} l_{45^{\circ}} & =\frac{20^2}{10}\left(2 \sin 45^{\circ} \operatorname{cos} 45^{\circ}\right) \\ & =40\left(2 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}\right) \\ & =40 \mathrm{~m} \end{aligned} $$
$$ \therefore \text { The best launching angle is } 45^{\circ} \text {. } $$