Question 14:
The depth of water in a watershed varies over time. When the height of the water reaches the maximum level, a water gate opens to release water until the water level returns to its minimum. Diagram 8 shows a complete cycle of the depth of water, in m, in the watershed.
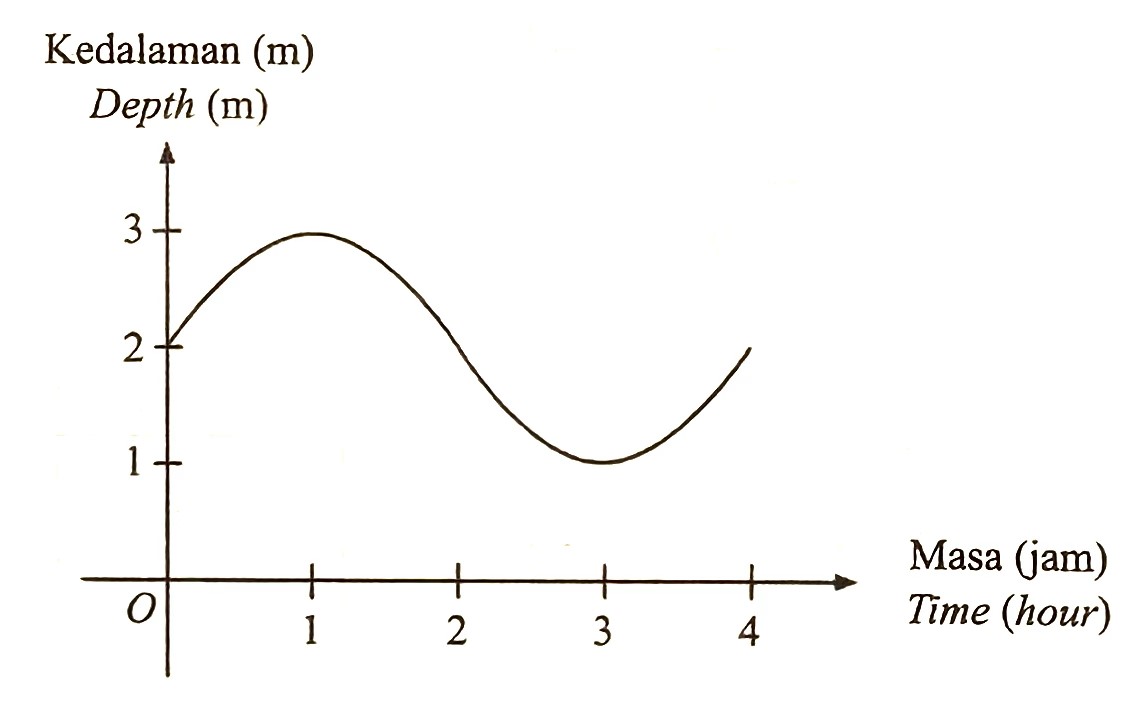
(a) Based on Diagram 8, state
(i) the minimum level, in m , of the water in the watershed. [1 mark]
(ii) the length of time, in hours, that the gate of the watershed is open. [1 mark]
(b)(i) Write down the equation of the graph in the form y = a sin bx + c where a, b and c are constants. [2 marks]
(ii) Hence, find the depth of water, in m, when the time is 150 minutes. [1 mark]
(c) During rainy season, the depth of the water will rise from the initial level to the maximum level faster. A complete cycle will happen every 2 hours.
(i) Complete the graph in the answer space for the depth of water during rainy season. [2 marks]
(ii) By comparing Diagram 8 and your graph in (c)(i), explain what the difference in frequency of both graphs means in the context of the question. [1 mark]
Solution:
(a)(i) From the graph, minimum level is 1 m.
(a)(ii)
From the graph, the length of time that the gate of the watershed is open
= 3 – 1
= 2 hours
(b)(i)
$$ \begin{aligned} &y=a \sin b x+c\\ &\text { Amplitude, } a=1 \end{aligned} $$
$$ \begin{aligned} &b=\frac{360}{4}=90\\ &c=2 \text {, the graph moves } 2 \text { units up }\\ &\begin{aligned} & y=(1) \sin (90) x+2 \\ & y=\sin 90 x+2 \end{aligned} \end{aligned} $$
(b)(ii)
$$ x=150 \text { minutes }=\frac{150}{60}=2.5 \text { hours } $$
$$ \begin{aligned} y & =\sin 90(2.5)+2 \\ & =-0.7071+2 \\ & =1.2929 \mathrm{~m} \end{aligned} $$
(c)(i)
Given that a complete cycle will happen every 2 hours.
$$ \begin{aligned} & b=\frac{360}{2}=180 \\ & y=\sin 180 x+2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(0)+2 \\ & y=0+2=2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(0.5)+2 \\ & y=1+2=3 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(1)+2 \\ & y=0+2=2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(1.5)+2 \\ & y=-1+2=1 \end{aligned} $$

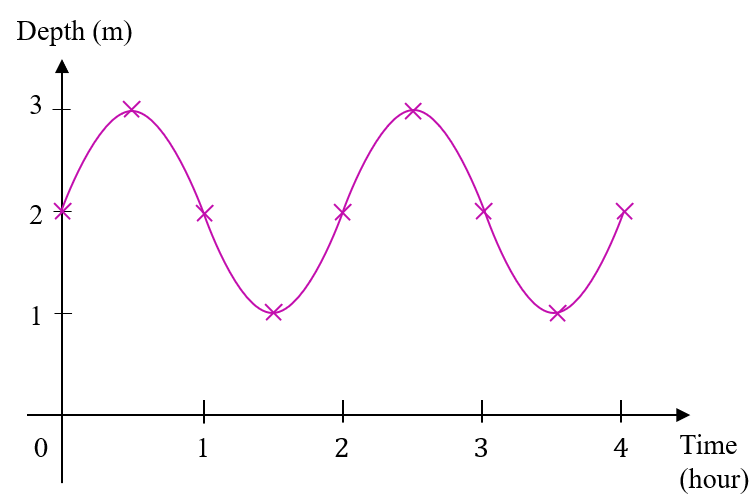
The depth of water in a watershed varies over time. When the height of the water reaches the maximum level, a water gate opens to release water until the water level returns to its minimum. Diagram 8 shows a complete cycle of the depth of water, in m, in the watershed.

(a) Based on Diagram 8, state
(i) the minimum level, in m , of the water in the watershed. [1 mark]
(ii) the length of time, in hours, that the gate of the watershed is open. [1 mark]
(b)(i) Write down the equation of the graph in the form y = a sin bx + c where a, b and c are constants. [2 marks]
(ii) Hence, find the depth of water, in m, when the time is 150 minutes. [1 mark]
(c) During rainy season, the depth of the water will rise from the initial level to the maximum level faster. A complete cycle will happen every 2 hours.
(i) Complete the graph in the answer space for the depth of water during rainy season. [2 marks]
(ii) By comparing Diagram 8 and your graph in (c)(i), explain what the difference in frequency of both graphs means in the context of the question. [1 mark]
Solution:
(a)(i) From the graph, minimum level is 1 m.
(a)(ii)
From the graph, the length of time that the gate of the watershed is open
= 3 – 1
= 2 hours
(b)(i)
$$ \begin{aligned} &y=a \sin b x+c\\ &\text { Amplitude, } a=1 \end{aligned} $$
$$ \begin{aligned} &b=\frac{360}{4}=90\\ &c=2 \text {, the graph moves } 2 \text { units up }\\ &\begin{aligned} & y=(1) \sin (90) x+2 \\ & y=\sin 90 x+2 \end{aligned} \end{aligned} $$
(b)(ii)
$$ x=150 \text { minutes }=\frac{150}{60}=2.5 \text { hours } $$
$$ \begin{aligned} y & =\sin 90(2.5)+2 \\ & =-0.7071+2 \\ & =1.2929 \mathrm{~m} \end{aligned} $$
(c)(i)
Given that a complete cycle will happen every 2 hours.
$$ \begin{aligned} & b=\frac{360}{2}=180 \\ & y=\sin 180 x+2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(0)+2 \\ & y=0+2=2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(0.5)+2 \\ & y=1+2=3 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(1)+2 \\ & y=0+2=2 \end{aligned} $$
$$ \begin{aligned} & y=\sin 180(1.5)+2 \\ & y=-1+2=1 \end{aligned} $$


(c)(ii) Diagram 8 shows the number of water releases in 4 hours is one time whereas Diagram (c)(i) shows the number of water releases in 4 hours is two times.