Question 9 (6 marks):
A bag contains five cards, labelled with the letters I, J, K, M and U.
One card is picked at random from the bag and the letter is recorded. Without replacement, another card is picked at random from the bag and the letter is also recorded.
(a) Complete the sample space in the answer space.
(b) By listing all the possible outcomes of the event, find the probability that
(i) the first card picked is labelled with a vowel.
(ii) the first card picked is labelled with a consonant and the second card picked is labelled with a vowel.
Answer:
{(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , )}
Solution:
(a)
S = {(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), (K, M), (K, U), (M, I), (M, J), (M, K), (M, U), (U, I), (U, J), (U, K), (U, M)}
(b)(i)
{(I, J), (I, K), (I, M), (I, U), (U, I), (U, J), (U, K), (U, M)}
(b)(ii)
{(J, I), (J, U), (K, I), (K, U), (M, I), (M, U)}
A bag contains five cards, labelled with the letters I, J, K, M and U.
One card is picked at random from the bag and the letter is recorded. Without replacement, another card is picked at random from the bag and the letter is also recorded.
(a) Complete the sample space in the answer space.
(b) By listing all the possible outcomes of the event, find the probability that
(i) the first card picked is labelled with a vowel.
(ii) the first card picked is labelled with a consonant and the second card picked is labelled with a vowel.
Answer:
{(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , )}
Solution:
(a)
S = {(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), (K, M), (K, U), (M, I), (M, J), (M, K), (M, U), (U, I), (U, J), (U, K), (U, M)}
(b)(i)
{(I, J), (I, K), (I, M), (I, U), (U, I), (U, J), (U, K), (U, M)}
(b)(ii)
{(J, I), (J, U), (K, I), (K, U), (M, I), (M, U)}
Question 10 (6 marks):
(a) Diagram 5.1 shows a Ferris wheel. The distance between point L and point M is 18 m.
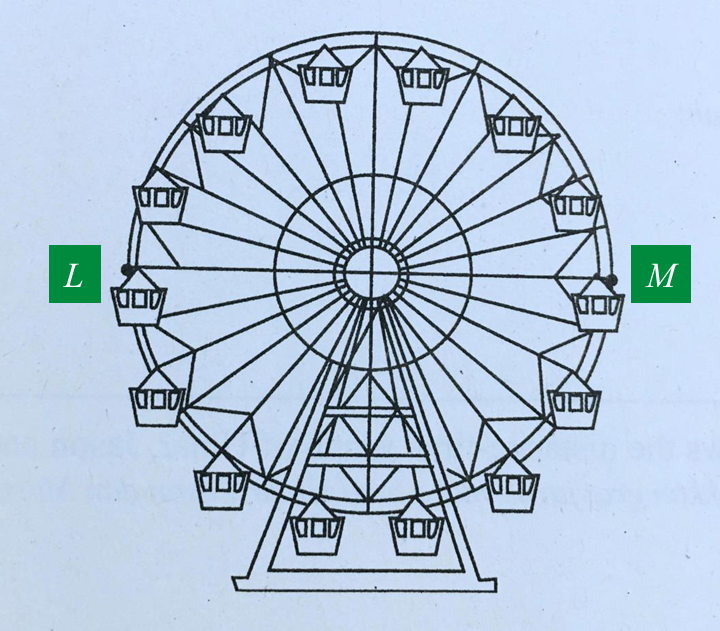 Diagram 5.1
Diagram 5.1
Calculate the minimum number of complete spins required to cover the distance of 600 m in a circular motion.
(b) Diagram 5.2 shows one large pizza and two small pizzas. Assume all pizzas are circular with a flat surface.
 Diagram 5.2
Diagram 5.2
Using , calculate the portion of the large pizza which equals to two small pizzas.
Solution:
(a)
(b)
(a) Diagram 5.1 shows a Ferris wheel. The distance between point L and point M is 18 m.
 Diagram 5.1
Diagram 5.1Calculate the minimum number of complete spins required to cover the distance of 600 m in a circular motion.
(b) Diagram 5.2 shows one large pizza and two small pizzas. Assume all pizzas are circular with a flat surface.
 Diagram 5.2
Diagram 5.2Using , calculate the portion of the large pizza which equals to two small pizzas.
Solution:
(a)
(b)