SPM Mathematics Trial 2021 (Selangor), Paper 2 (Question 7 & 8)

Question 7:
For this question, give all your answers as fractions..
When Ivan goes to shopping mall, the probability that he wears a hat is 5/8. If he wears a hat, then the probability that he wears sport shoes is 2/3. If he does not wear a hat, then the probability that he wears sport shoes is 1/6.

(a) Diagram 4 in the answer space shows all the possible outcomes. Complete the tree diagram in Diagram 4. [2 marks]


(b) Hence, find the probability that Ivan wears a hat or sport shoes but not both. [2 marks]


Solution:
(a)



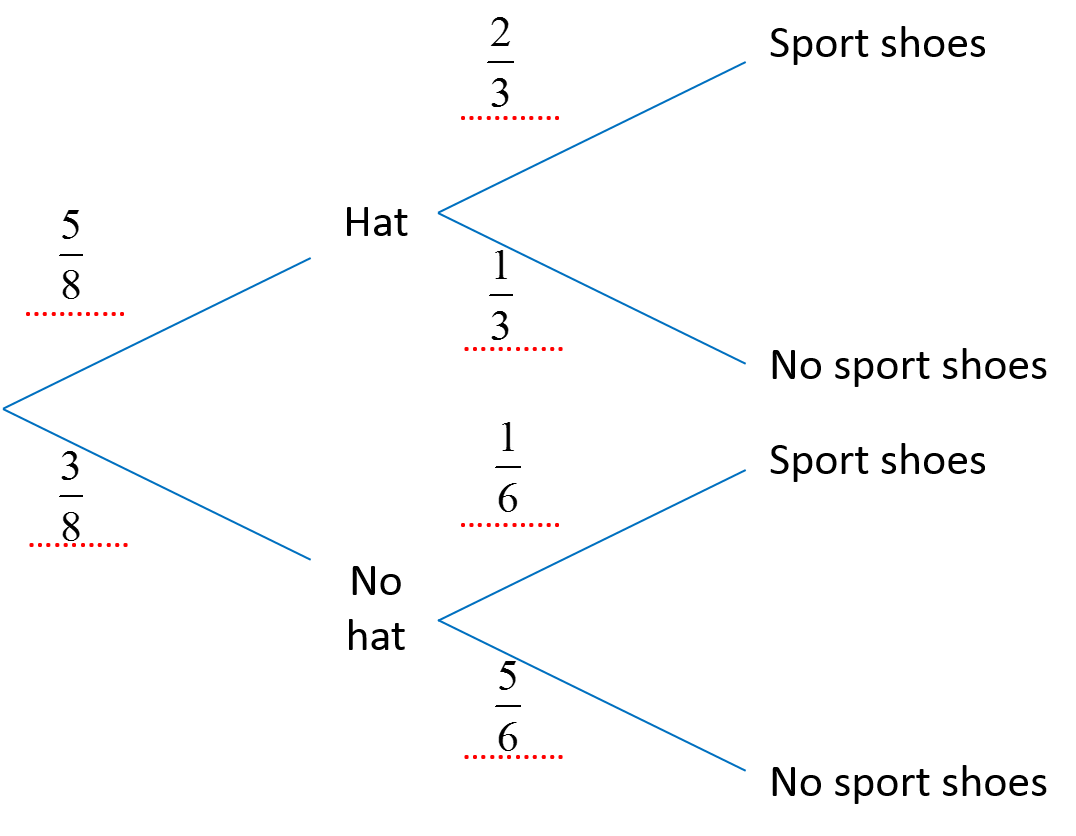
(b)

$\begin{array}{l}\text{Probability that Ivan wears a hat or sport shoes}\\ =P\left(\text{Hat, no sport shoes}\right)+P\left(\text{No hat, wears sport shoes}\right)\\ =\left(\frac{5}{8}\times \frac{1}{3}\right)+\left(\frac{3}{8}\times \frac{1}{6}\right)\\ =\frac{13}{48}\end{array}$

Question 8:
Firdaus is training for a marathon. He practises according to his routine which is running as far as 32 km a week. He plans to increase his running distance, D(x), in km, each week by 10% of his running distance in the previous week, where x represents number of weeks of training.
Derive a mathematical model for his running distance, D(x) through mathematical modeling.
[4 marks]


Solution:

$10\%=\frac{10}{100}=0.1$
D(x) = 32(1.1)^x

Week	Calculation (km)	Running distance (km)
1	32 + 32 × 0.1 = 32(1 + 0.1)	3.2 (1.1)
2	32(1.1) + 32(1.1) × 0.1 = 32(1.1)(1 + 0.1)	3.2 (1.1)2
3	32(1.1)2 + 32(1.1)2 × 0.1 = 32(1.1)2 (1 + 0.1)	3.2 (1.1)3
4	32(1.1)3 + 32(1.1)3 × 0.1 = 32(1.1)3 (1 + 0.1)	3.2 (1.1)4