SPM Mathematics 2018, Paper 2 (Questions 3 & 4)

Question 3 (4 marks):
Diagram 3 shows a garden path with a rectangular shape. There are 8 similar circular stepping stone built in the path.


Given the area of the path is 32 m², find the diameter, in m, of one piece of stepping stone.

Solution:
$\begin{array}{l}\text{Given the area of the path}\\ =32{\text{ m}}^2=320000{\text{ cm}}^2\\ x\left(x+4\right)=320000\\ x^2+4x-320000=0\\ a=1,b=4,c=-320000\\ x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\\ x=\frac{-4\pm \sqrt{4^2-4\left(1\right)\left(-320000\right)}}{2\left(1\right)}\\ x=\frac{-4\pm \sqrt{1280016}}{2}\\ x=\frac{-4+1131.38}{2}\text{ or }\frac{-4-1131.38}{2}\\ x=563.69\text{ or }-567.69\left(\text{ignored}\right)\\ \\ \text{Diameter of one piece of stepping}\\ \text{stone}=x\\ =563.69\text{ cm}\\ =5.64\text{ m}\end{array}$

Question 4 (4 marks):
Diagram 4 shows a composite solid formed by joining a quarter cylinder and a cuboid which lies on the horizontal plane.


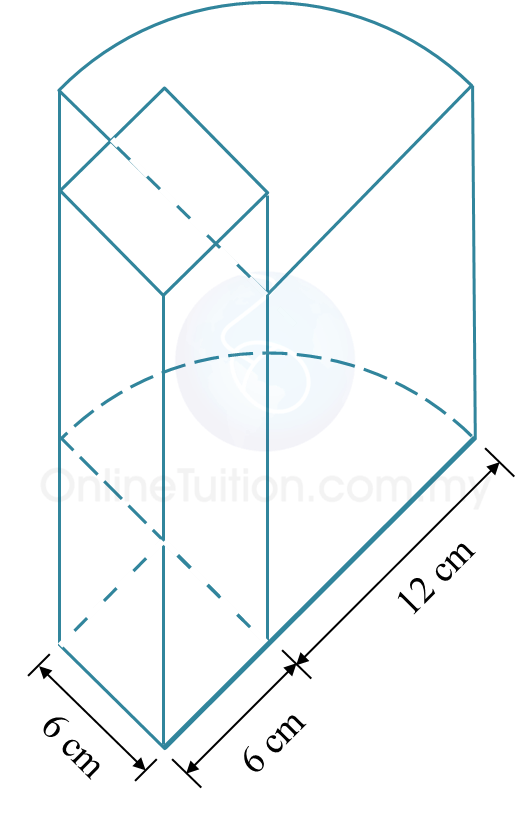
It is given that the height of the cuboid is 9 cm and the volume of the composite solid is $1002\frac{6}{7}{\text{ cm}}^3.$  
Using $\pi =\frac{22}{7}$ , calculate the height, in cm, of the quarter cylinder.


Solution:
$\begin{array}{l}V\text{ cuboid}+\frac{1}{4}\left(V\text{ cylinder}\right)=1002\frac{6}{7}\\ \left(6\times 6\times 9\right)+\frac{1}{4}\left(\frac{22}{7}\times {12}^2\times t\right)=\frac{7020}{7}\\ 324+\frac{792}{7}t=\frac{7020}{7}\\ \frac{792}{7}t=\frac{4752}{7}\\ t=6\\ \\ \text{Height of the quarter cylinder}=6\text{ cm}\end{array}$