Question 7:
Diagram below shows 4 cards labelled with letters.

Two cards are chosen at random from the box, one by one, without replacement.
(a) List the sample space.
(b) Find the probability that
(i) at least one card chosen is labelled C,
(ii) both cards chosen are labelled with same letter.
Solution:
(a)
Sample space, S
= {(C, O1), (C, O2), (C, L), (O1, C), (O1, O2), (O1, L), (O2, C), (O2, O1), (O2, L), (L, C), (L, O1), (L, O2)}
n(S) = 12
(b)(i)
At least one card chosen is labelled C
= {(C, O1), (C, O2), (C, L), (O1, C), (O2, C), (L, C)}
(b)(ii)
Both cards chosen are labelled with same letter
= {(O1, O2), (O2, O1)}
Diagram below shows 4 cards labelled with letters.

Two cards are chosen at random from the box, one by one, without replacement.
(a) List the sample space.
(b) Find the probability that
(i) at least one card chosen is labelled C,
(ii) both cards chosen are labelled with same letter.
Solution:
(a)
Sample space, S
= {(C, O1), (C, O2), (C, L), (O1, C), (O1, O2), (O1, L), (O2, C), (O2, O1), (O2, L), (L, C), (L, O1), (L, O2)}
n(S) = 12
(b)(i)
At least one card chosen is labelled C
= {(C, O1), (C, O2), (C, L), (O1, C), (O2, C), (L, C)}
(b)(ii)
Both cards chosen are labelled with same letter
= {(O1, O2), (O2, O1)}
Diagram Diagram 8.1 shows three cards labelled with letters in bag A and three numbered cards in bag B.
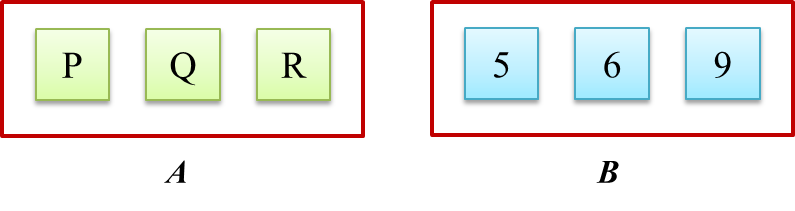
Diagram 8.1
A card is picked at random from bag A and then a card is picked at random from bag B.
(a) Diagram 8.2 in the answer space shows the incomplete possible outcomes of the event.
Complete the possible outcomes in Diagram 8.2.
(b) Using the complete possible outcomes in 10(a), find the probability that
(i) a card labelled Q and the card with odd number are picked,
(ii) a card labelled P or the card with a number which is multiple of 3 are picked.
[5 marks]
Answer:
(a)


Diagram 8.2
Solution:
(a)
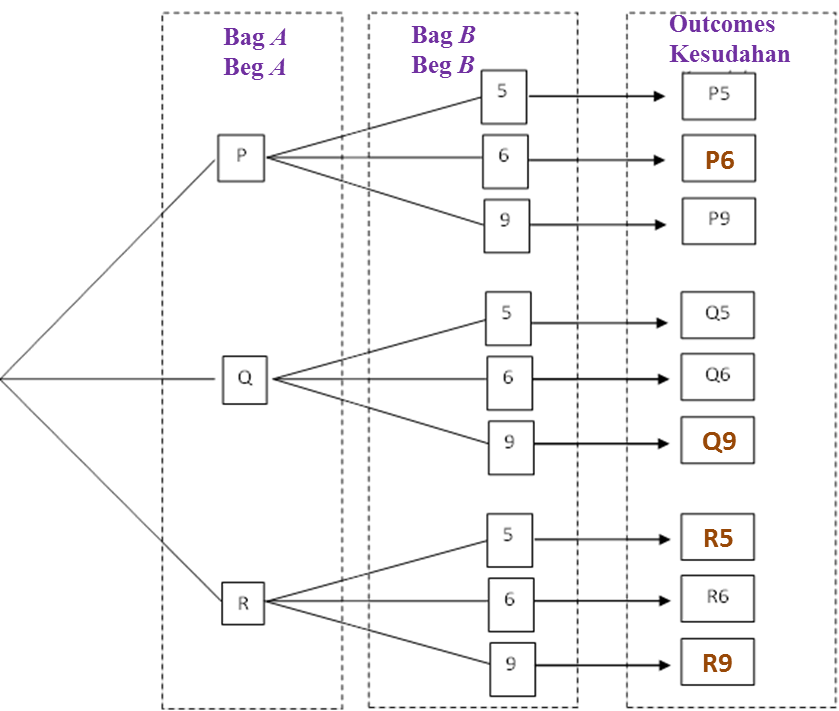

(b)(i)
n (s) = 9
P (a card labelled Q and a card with odd number)
= {(Q 5), (Q 9)}
(b)(ii)
P (a card labelled P or a card with a number which is multiple of 3)
= {(P 5), (P 6), (P 9), (Q 6), (Q 9), (R 6), (R 9)}
VERY USEFUL AND GOOD QUESTIONS FOR PRACTICE. THANK YOU.