Question 1:
Solution:
(a)
• (X υ Y’) means the union of the region X and the region outside Y.
• The region then intersects with region Z to give the result of (X υ Y’) ∩ Z.
The Venn diagrams in the answer space shows sets X, Y and Z such that the universal set,
On the diagrams in the answer space, shade
Solution:
(a)
• X’ ∩ Y means the intersection of the region outside X with the region Y.
(b)
• Find the region of (X υ Y’) first.• (X υ Y’) means the union of the region X and the region outside Y.
• The region then intersects with region Z to give the result of (X υ Y’) ∩ Z.
Question 2:
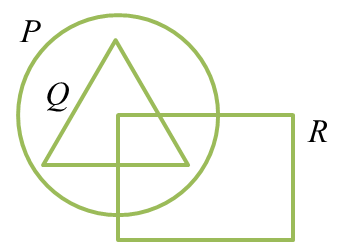
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ = P υ Q υ R
On the diagrams in the answer space, shade
(a) Q ∩ R,
(b) (P’ ∩ R) υ Q.
Solution:
(a)
• Q ∩ R means the intersection of the region Q and the region R.
(b)
• Find the region of (P’ ∩ R) first.
• (P’ ∩ R) means the region that is outside P and is inside R.
• The union of this region with region Q give the result of (P’ ∩ R) υ Q.
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ = P υ Q υ R
On the diagrams in the answer space, shade
(a) Q ∩ R,
(b) (P’ ∩ R) υ Q.
Solution:
(a)
• Q ∩ R means the intersection of the region Q and the region R.
(b)
• Find the region of (P’ ∩ R) first.
• (P’ ∩ R) means the region that is outside P and is inside R.
• The union of this region with region Q give the result of (P’ ∩ R) υ Q.