1.3 Quadratic Equations
1. Quadratic equations are equations which fulfil the following characteristics:
(a) Have an equal ‘=’ sign
(b) Contain only one unknown
(c) Highest power of the unknown is 2.
For example,
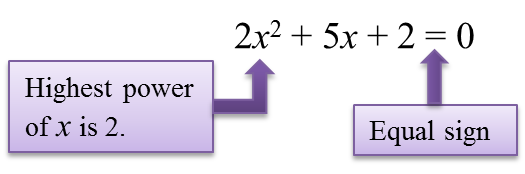

2. The general form of a quadratic equation is written as:
(a)
ax2 + bx + c = 0,
ax2 + bx + c = 0,
where a ≠ 0, b ≠ 0 and c ≠ 0,
example: 4x2+ 13x – 12 = 0
(b)
ax2 + bx = 0,
where a ≠ 0, b ≠ 0 but c = 0,
example: 7x2+ 9x = 0
(c)
ax2 + c = 0,
where a ≠ 0, c ≠ 0 but b = 0,
example: 9x2– 3 = 0
Example 1:
(b) –2 + 5x2– 6x = 0
(c) 7p2 – 3p = 4p2+ 4p – 3
(d) (x – 2)(x + 6) = 0
(e) 3 – 13x = 4 (x2 + 2)
(f)
(g)
(h)
(i)
Write each quadratic equation in the general form.
(a) x2 – 5x = 12
(b) -2 + 5x2– 6x = 0
(c) 7p2 – 3p = 4p2+ 4p – 3
(d) (x – 2)(x + 6) = 0
(e) 3 – 13x = 4 (x2 + 2)
(f)
(g)
(h)
(i)
Solution:
(g)
(h)
(i)
Solution:
A quadratic equation in the general form is written as ax2 + bx + c = 0
(a) x2 – 5x = 12
x2 – 5x -12 = 0
(b) –2 + 5x2– 6x = 0
5x2 – 6x –2 = 0
(c) 7p2 – 3p = 4p2+ 4p – 3
7p2 – 3p – 4p2– 4p + 3 = 0
3p2 – 7p + 3 = 0
(d) (x – 2)(x + 6) = 0
x2 + 6x – 2x– 12 = 0
x2 + 4x – 12 = 0
(e) 3 – 13x = 4 (x2 + 2)
3 – 13x = 4x2 + 8
–4x2 – 8 + 3 – 13x = 0
–4x2 – 13x – 5 = 0
4x2 + 13x + 5 = 0
(f)
2y – y2 = 1 – 3y
2y – y2 – 1 + 3y = 0
– y2 + 5y – 1 = 0
y2 – 5y + 1 = 0
(g)
10p = 8p2 – 12
–8p2 + 10p +12 = 0
8p2 – 10p – 12 = 0
(h)
2y2 + 10 = 4y – 4
2y2 – 4y + 10 + 4 = 0
2y2 – 4y + 14 = 0
2y2 – 4y + 14 = 0
(i)
4p = 7p (7p– 6)
4p = 49p2 – 42p
– 49p2 + 42p + 4p = 0
49p2 – 46p = 0
Example 1 Q) f, the solution how come is 3y not 5y???!~
Dear Gabriel,
Thanks for pointing out our mistake, correction had been made accordingly.