SPM Mathematics 2016, Paper 2 (Questions 13 & 14)

Question 13 (12 marks):
Diagram 13.1 shows three triangles RPQ, UST and RVQ, drawn on a Cartesian plane.
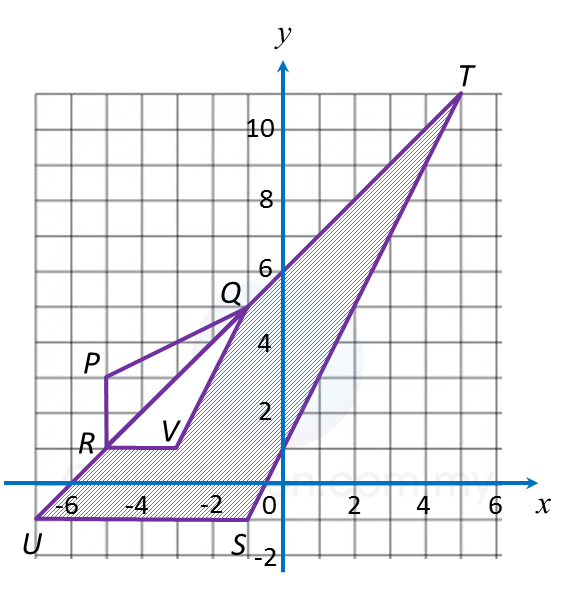Diagram 13.1

(a) Transformation R is a rotation of 90^o, clockwise about the centre O.
Transformation T is a translation $\left(\begin{array}{l}2\\ \text{3}\end{array}\right)$ .
State the coordinates of the image of point B under each of the following transformations:
(i) Translation T²,
(ii) Combined transformation TR.

(b)
(i) Triangle UST is the image of triangle RPQ under the combined transformation VW.
Describe in full the transformation:
(a) W   (b) V

(ii) It is given that quadrilateral RPQ represents a region of area 15 m².
Calculate the area, in m², of the region represented by the shaded region.

Solution:


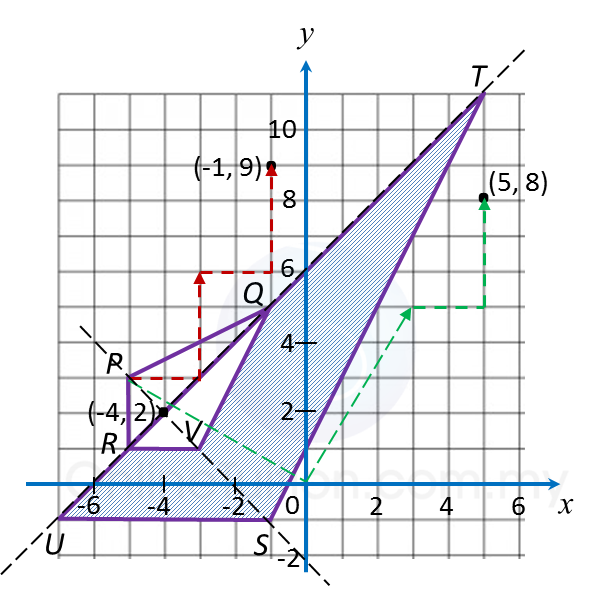
(a)
(i) (–5, 3) → T → (–3, 6) ) → T → (–1, 9)
(ii) (–5, 3) → R → (3, 5) → T → (5, 8)

(b)(i)(a)
W: A reflection in the line URQT.

(b)(i)(b)
$\begin{array}{l}\text{Scale factor}=\frac{US}{RV}=\frac{6}{2}=3\\ \text{V: An enlargement of scale factor 3 at centre }\left(-4,2\right)\end{array}$

(b)(ii)
Area of UST = (Scale factor)² x Area of RPQ
= 3² x area of RPQ
= 3² x 15
= 135 m²

Therefore,
Area of the shaded region
= Area of UST – area of RPQ
= 135 – 15
= 120 m²

Question 14 (12 marks):
Diagram 14 shows a histogram which represents the mass, in kg, for a group of 100 students.

Diagram 14

(a) Based on Diagram 14, complete Table 14 in the answer space.

(b) Calculate the estimated mean mass of a student.

(c) For this part of the question, use graph paper. You may use a flexible curve ruler.
Using a scale of 2 cm to 10 kg on the horizontal axis and 2 cm to 10 students on the vertical axis, draw an ogive for the data.

(d) Based on the ogive drawn in 14(c), state the third quartile.

Answer:



Solution:
(a)


(b)


$\begin{array}{l}\text{Estimated mean mass}\\ =\frac{8110}{100}\\ =81.1\text{ kg}\end{array}$

(c)



(d)
Third quartile
= 75th student
= 90.0 kg