Question 1:
(a) State whether each of the following sentences is a statement or not a statement.
(i) 4 is a multiple of 2.
(ii) y = 2x + 5
[2 marks]
(b) Diagram 1 shows an implication.
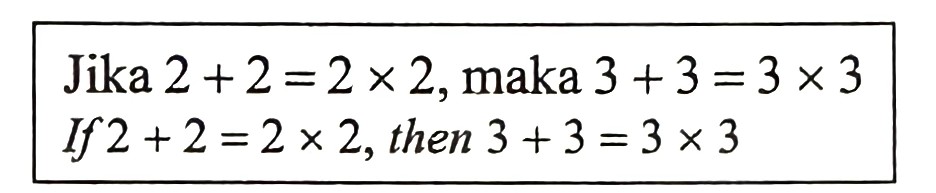
(i) Write down the inverse of the implication.
(ii) Hence, determine the truth value of the inverse.
[2 marks]
Answer:
(a)(i) Statement
(a)(ii) Not a statement
(b)(i)
$$ \text { If } 2+2 \neq 2 \times 2 \text {, then } 3+3 \neq 3 \times 3 $$
(b)(ii) True
(a) State whether each of the following sentences is a statement or not a statement.
(i) 4 is a multiple of 2.
(ii) y = 2x + 5
[2 marks]
(b) Diagram 1 shows an implication.
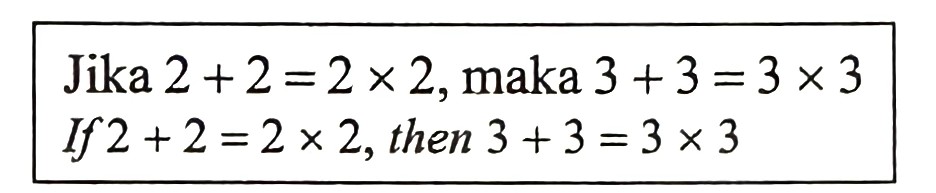
(i) Write down the inverse of the implication.
(ii) Hence, determine the truth value of the inverse.
[2 marks]
Answer:
(a)(i) Statement
(a)(ii) Not a statement
(b)(i)
$$ \text { If } 2+2 \neq 2 \times 2 \text {, then } 3+3 \neq 3 \times 3 $$
(b)(ii) True
Question 2:
Table 1 shows the values of function y = –x2 + 4 for -3 ≤ x ≤ 2.

In the answer space, draw the graph of y = –x2 + 4 for -3 ≤ x ≤ 2. You may use a flexible curve rule.
[3 marks]
Answer:

Answer:
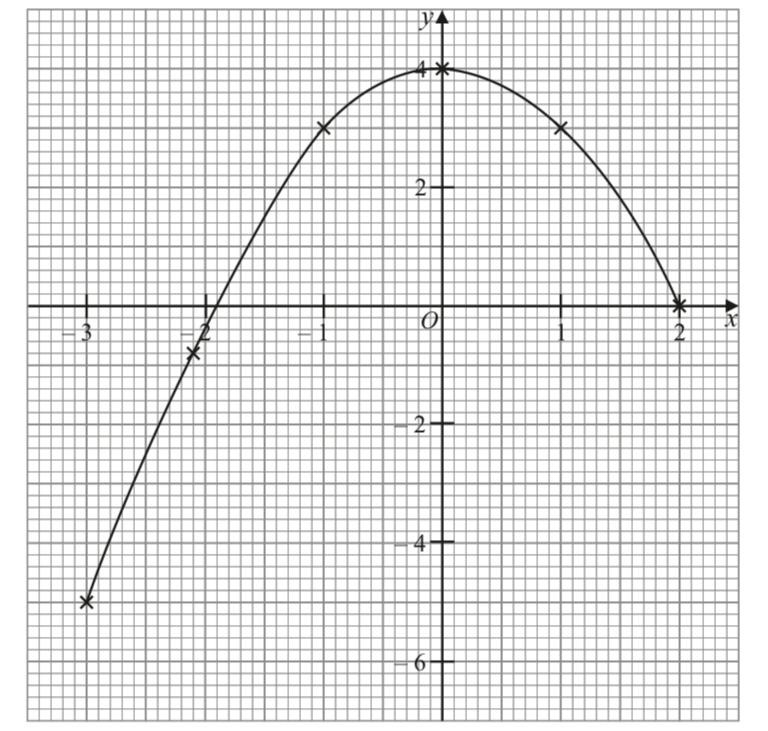
Table 1 shows the values of function y = –x2 + 4 for -3 ≤ x ≤ 2.

In the answer space, draw the graph of y = –x2 + 4 for -3 ≤ x ≤ 2. You may use a flexible curve rule.
[3 marks]
Answer:

Answer:
