8.2.4 Variance and Standard Deviation

Variance and Standard Deviation

1. The variance is a measure of the mean for the square of the deviations from the mean.

2. The standard deviation refers to the square root for the variance.

(A) Ungrouped Data

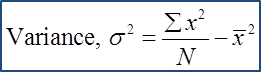
Example 1:

Find the variance and standard deviation of the following data.

15, 17, 21, 24 and 31

Solution:

\begin{array}{l} Variance, σ^{2} = \frac{\sum x^{2}}{N} - {\bar{x}}^{2} \\ σ^{2} = \frac{15^{2} + 17^{2} + 21^{2} + 24^{2} + 31^{2}}{5} \\ - {(\frac{15 + 17 + 21 + 24 + 31}{5})}^{2} \\ σ^{2} = \frac{2492}{5} - {21.6}^{2} \\ σ^{2} = 31.84 \\ Standard deviation, σ = \sqrt{variance} \\ σ = \sqrt{31.84} \\ σ = 5.642 \end{array}