Question 3:
(a) Transformation P is a reflection in the line x = m.
Transformation T is a translation
.
Transformation R is a clockwise rotation of 90o about the centre (0, 4).
(i) The point (6, 4) is the image of the point ( –2, 4) under the transformation P.
State the value of m.
(ii) Find the coordinates of the image of point (2, 8) under the following combined transformations:
(a) T2,
(b) TR.
(b) Diagram below shows trapezium CDFE and trapezium HEFG drawn on a Cartesian plane.
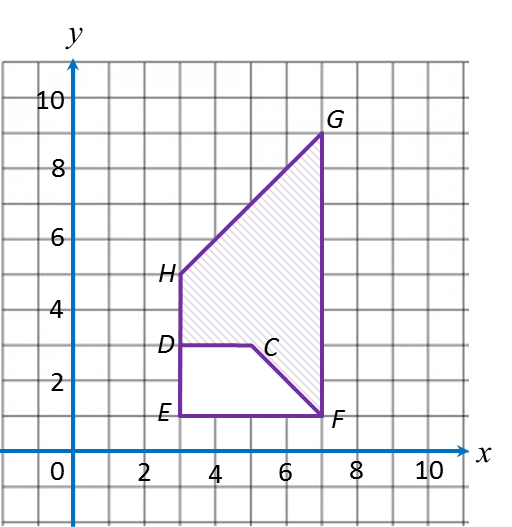
(i) HEFG is the image of CDEF under the combined transformation WU.
Describe in full the transformation:
(a) U (b) W
(ii) It is given that CDEF represents a region of area 60 m2.
Calculate the area, in m2, of the region represented by the shaded region.
Solution:
(a)(i)
(a)(ii)
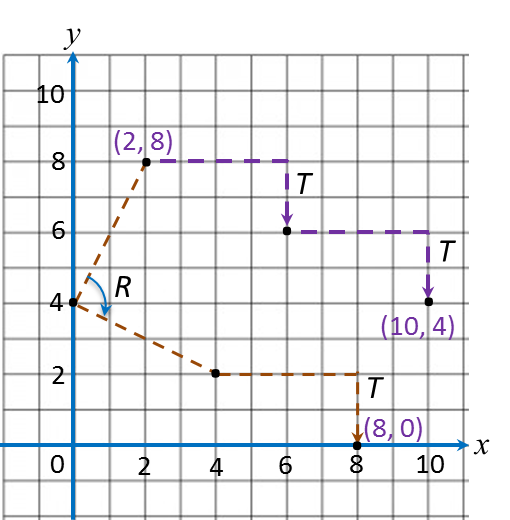
(a) (2, 8) → T → (6, 6) → T → (10, 4)
(b) (2, 8) → R → (4, 2) → T → (8, 0)
(b)(i)(a)
U: An anticlockwise rotation of 90oabout the centre A (3, 3).
(b)(i)(b)
W: An enlargement of scale factor 2 with centre B (3, 5).
(b)(ii)
Area of HEFG= (Scale factor)2 × Area of object
= 22 × area of CDEF
= 4 × 60
= 240 m2
Therefore,
Area of the shaded region
= Area of HEFG– area of CDEF
= 240 – 60
= 180 m2
Question 4:
Diagram below shows three triangles RPQ, UST and RVQ, drawn on a Cartesian plane.
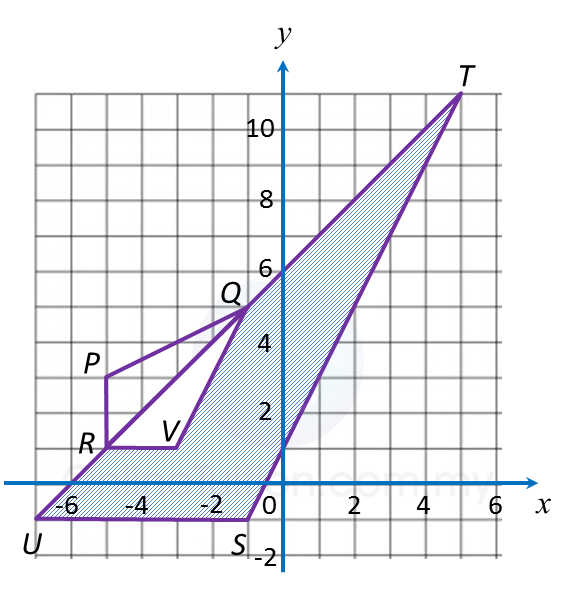
(a) Transformation R is a rotation of 90o, clockwise about the centre O.
Transformation T is a translation .
State the coordinates of the image of point B under each of the following transformations:
(i) Translation T2,
(ii) Combined transformation TR.
(b)
(i) Triangle UST is the image of triangle RPQ under the combined transformation VW.
Describe in full the transformation:
(a) W (b) V
(ii) It is given that quadrilateral RPQ represents a region of area 15 m2.
Calculate the area, in m2, of the region represented by the shaded region.
Solution:
(a)
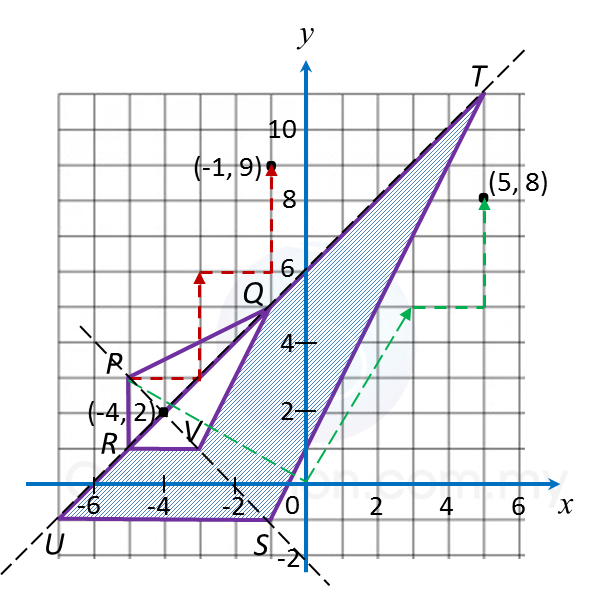
(i) (–5, 3) → T → (–3, 6) ) → T → (–1, 9)
(ii) (–5, 3) → R → (3, 5) → T → (5, 8)
(b)(i)(a)
W: A reflection in the line URQT.
(b)(i)(b)
(b)(ii)
Area of UST = (Scale factor)2 x Area of RPQ
= 32 x area of RPQ
= 32 x 15
= 135 m2
Therefore,
Area of the shaded region
= Area of UST – area of RPQ
= 135 – 15
= 120 m2
Diagram below shows three triangles RPQ, UST and RVQ, drawn on a Cartesian plane.

(a) Transformation R is a rotation of 90o, clockwise about the centre O.
Transformation T is a translation .
State the coordinates of the image of point B under each of the following transformations:
(i) Translation T2,
(ii) Combined transformation TR.
(b)
(i) Triangle UST is the image of triangle RPQ under the combined transformation VW.
Describe in full the transformation:
(a) W (b) V
(ii) It is given that quadrilateral RPQ represents a region of area 15 m2.
Calculate the area, in m2, of the region represented by the shaded region.
Solution:

(a)
(i) (–5, 3) → T → (–3, 6) ) → T → (–1, 9)
(ii) (–5, 3) → R → (3, 5) → T → (5, 8)
(b)(i)(a)
W: A reflection in the line URQT.
(b)(i)(b)
(b)(ii)
Area of UST = (Scale factor)2 x Area of RPQ
= 32 x area of RPQ
= 32 x 15
= 135 m2
Therefore,
Area of the shaded region
= Area of UST – area of RPQ
= 135 – 15
= 120 m2