3.3 Operations on Statements
(A) Nagating a Statement using ‘No’ or ‘Not’
1. Negation of a statement refers to changing the truth value of the statement, that is, changing a true statement to a false statement and vice versa, using the word ‘not’ or ‘no’.
Example 1:
Change the true value of the following statements by using ‘no’ or ‘not’.
(a) 17 is a prime number.
(b) 39 is a multiple of 9.
Solution:
(a) 17 is not a prime number. (True to false)
(b) 39 not is a multiple of 9. (False to true)
2. A compound statement can be formed by combining two given statements using the word ‘and’.
Example 2:
Example 3:
Identify two statements from each of the following compound statements.
(a) All pentagons have 5 sides and 5 vertices.
(b) 33 = 27 and 43 = 64
Solution:
(a) All pentagons have 5 sides.
All pentagons have 5 vertices.
(b) 33 = 27
43 = 64Example 3:
Form a compound statement from each of the following pairs of statements using the word ‘and’.
(a) 19 is a prime number.
19 is an odd number.
(b) 15 – 5 = 10
15 × 5 = 75
Solution:
(a) 19 is a prime number and an odd number. ← (Repeated words can be eliminated when combining two statements using ‘and’.)
(b) 15 – 5 = 10 and15 × 5 = 75.
3. A compound statement can also be formed by combining two given statements using the word ‘or’.
Example 4:
Form a compound statement from each of the following pairs of statements using the word ‘or’.
(a) 11 is an odd number.
11 is a prime number.
Solution:
(a) 11 is an odd number or a prime number.
(B) Truth Values of Compound Statements using ‘And’
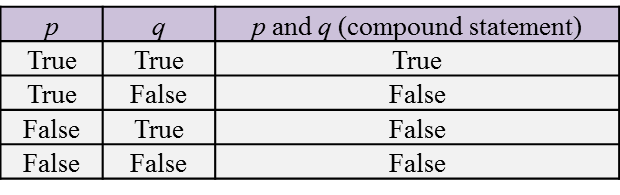
4. When two statements are combined using ‘and’, a true compound statement is obtained only if both statements are true.
5. If one or both statements are false, then the compound statement is false.
The truth table:
Let p = statement 1 and q = statement 2.
The truth values for ‘p’ and ‘q’ are as follows:

Example 5:
Determine the truth value of the following statements.
(a) 12 × (–3) = –36 and 15 – 7 = 8.
(b) 5 > 3 and –4 < –5.
(c) Hexagons have 5 sides and each of the interior angles is 90o.
Solution:
(a)
12 × (–3) = –36 ← (p is true)
15 – 7 = 8 ← (q is true)
Therefore 12 × (–3) = –36 and 15 – 7 = 8 is a true statement. (‘p and q’ is true)
(b)
5 > 3 ← (p is true)
–4 < –5 ← (q is false)
Therefore 5 > 3 and –4 < –5 is a false statement. (‘p and q’ is false)
(c)
Hexagons have 5 sides. ← (p is false)
Each of the interior angles of Hexagon is 90o. ← (q is false)
Therefore Hexagons have 5 sides and each of the interior angles is 90o is a false statement. (‘p and q’ is false)
(C) Truth Values of Compound Statements using ‘Or’
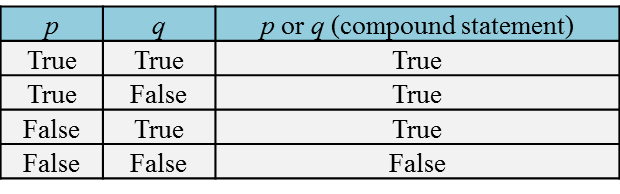
1. When two statements are combined using ‘or’, a false compound statement is obtained only if both statements are false.
2. f one or both statements are true, then the compound statement is true.
The truth table:
Let p = statement 1 and q= statement 2.
The truth values for ‘p’ or ‘q’ are as follows:
Example 6:
Determine the truth value of the following statements.
(a) 60 is divisible by 4 or 9.
(b) 53 = 25 or 43 = 64.
(c) 5 + 7 > 14 or √9 = 2.
Solution:
(a)
60 is divisible by 4 ← (p is true)
60 is divisible by 9 ← (q is false)
Therefore, 60 is divisible by 4 or 9 is a true statement. (‘p or q’ is true)
(b)
53 = 25 ← (p is false)
43 = 64 ← (q is true)
Therefore, 53 = 25 or 43 = 64 is a true statement. (‘p or q’ is true)
(c)
5 + 7 > 14 ← (p is false)
√9 = 2 ← (q is false)
Therefore, 5 + 7 > 14 or √9 = 2 is a false statement. (‘p or q’ is false)
Question 3 Example 4: odd number not old number
Dear Previgna,
thanks for pointing out our mistake, correction had been made accordingly.
typo nagating–>negating