Question 4:

Solution:
(a)
(b)
Average speed for the whole journey
=Total distance travelledTotal time taken=7510=7.5ms−1

The diagram above shows the speed-time graph of a moving particle for 10 seconds. From the graph above, find
(a) the total distance travel by the particle for the whole journey.
(b) the average speed for the whole journey.
(a)
Total distance travelled
= Area under the speed-time graph
= Area of triangle
= ½ × 15 × 10
= 75 m(b)
Average speed for the whole journey
=Total distance travelledTotal time taken=7510=7.5ms−1
Question 5:
Solution:
(a)
(b)
(c)

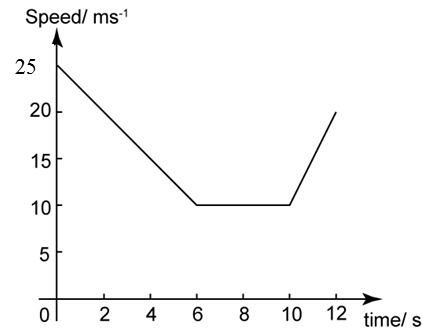
The diagram above shows the speed-time graph of a moving particle for 12 seconds. Find
(a) the length of the time, in s that the particle move with uniform speed.
(b) the distance travel by the particle when it move with constant speed.
(c) the distance travel by the particle when the rate of the speed change is negative.
Solution:
(a)
Length of the time the particle move with uniform speed
= 10 – 6
= 4 s
(b)
Distance travel by the particle when it move with constant speed
= Area under the speed-time graph
= Area of rectangle
= 4 × 10
= 40 m
(c)
Distance travel by the particle when the rate of the speed change is negative
= Area under the speed-time graph for the first 6 s
= Area of trapezium
= ½ (10 + 25)(6)
= 105 mQuestion 6:
Diagram below shows the speed-time graph for the movement of an object for a period of 40 seconds.
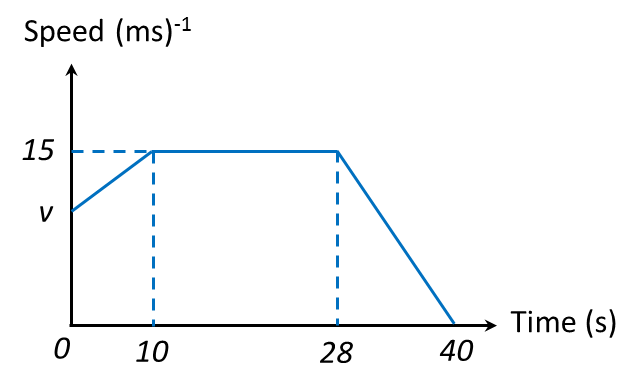
(a) State the duration of time, in s, for which the object moves with uniform speed.
(b) Calculate the rate of change of speed, in ms-2, of the object for the last 12 seconds.
(c) Calculate the value of v, if the total distance travelled for the period of 40 seconds is 500 m.
Solution:
(a) Duration of time the object moves with uniform speed = 28s – 10s = 18s
(b)Rate of change of speed=−1512ms−2=−1.25 ms−2(c)Area of trapezium I + Area of trapezium II=50012(v+15)10+12(18+30)15=500 5v+75+360=5005v=65 v=13
Diagram below shows the speed-time graph for the movement of an object for a period of 40 seconds.

(a) State the duration of time, in s, for which the object moves with uniform speed.
(b) Calculate the rate of change of speed, in ms-2, of the object for the last 12 seconds.
(c) Calculate the value of v, if the total distance travelled for the period of 40 seconds is 500 m.
Solution:
(a) Duration of time the object moves with uniform speed = 28s – 10s = 18s
(b)Rate of change of speed=−1512ms−2=−1.25 ms−2(c)Area of trapezium I + Area of trapezium II=50012(v+15)10+12(18+30)15=500 5v+75+360=5005v=65 v=13