Question 13:
(a) Diagram 10.1 is a Venn diagram that shows the favourite activities of three students. It is given that
universal set, ξ = A ∪ B ∪ C,
set A = {Azmil’s favourite activities},
set B = {Beng’s favourite activity},
set C = {Canny’s favourite activities}.
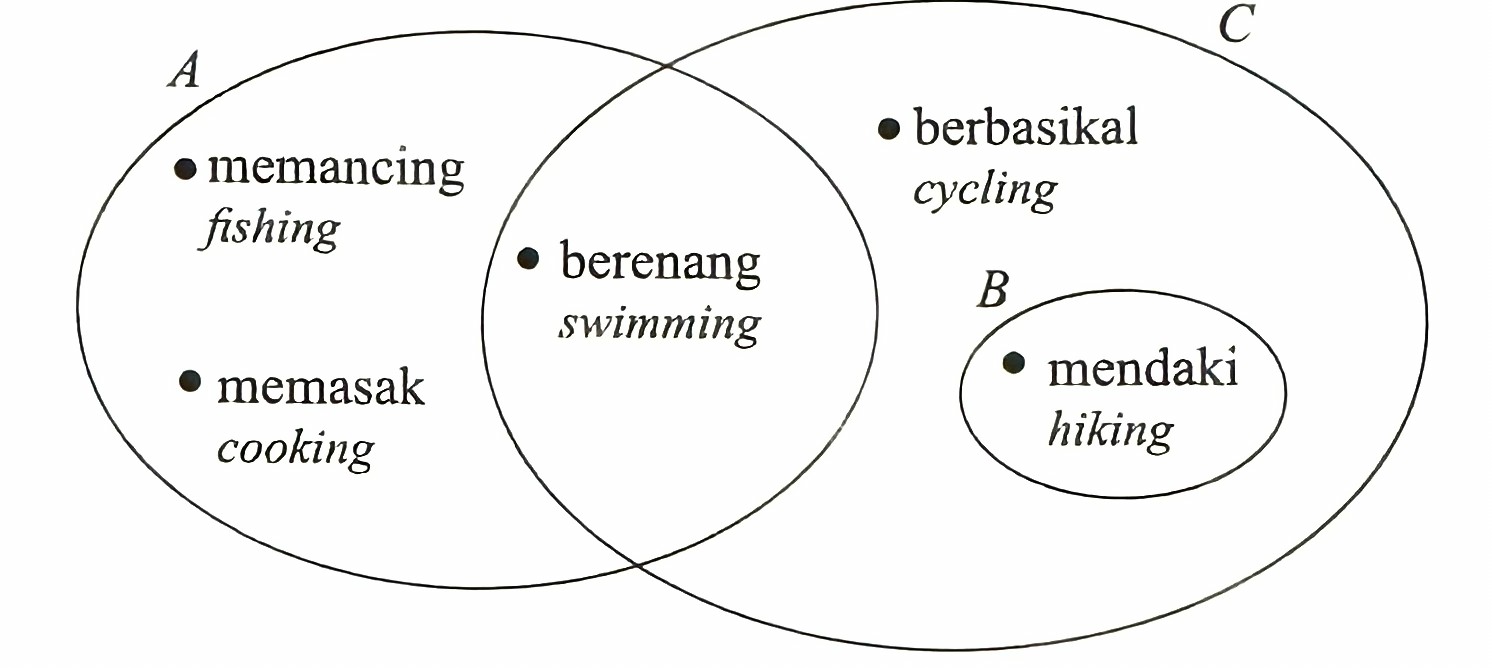
(i) Using the set notation, list the activities that are
(a) Azmil’s favourite activities only,
(b) Canny’s favourite activities but not Beng’s favourite activity.
[2 marks]
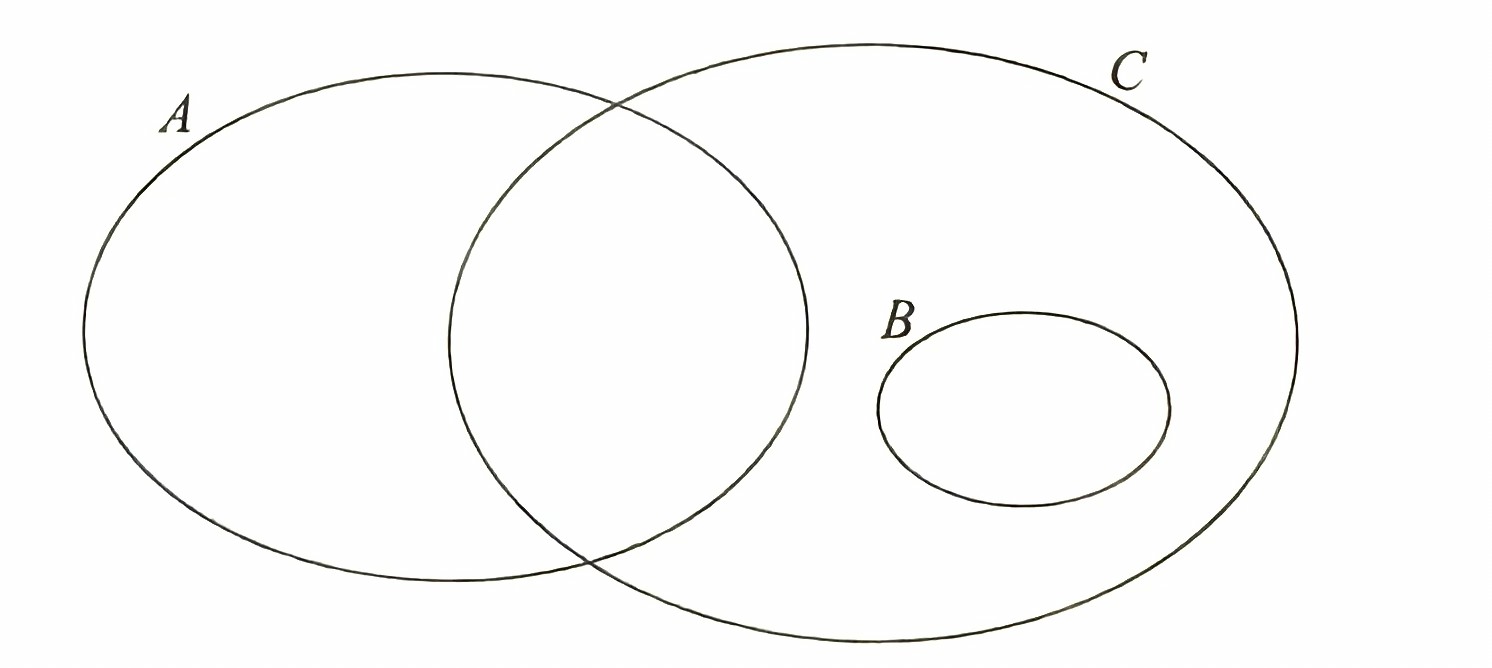
(ii) On the diagram in the answer space, shade the set C ∩ B‘.
[1 mark]
Answer:
(a)(ii)
(b) The Venn diagram as shown in Diagram 10.2 represents the number of students taking part in activities at a camp. In the Venn diagram,
universal set, ξ = {all students at the camp},
set F = {students taking part in fishing},
set C = {students taking part in cooking},
set H = {students taking part in hiking}.
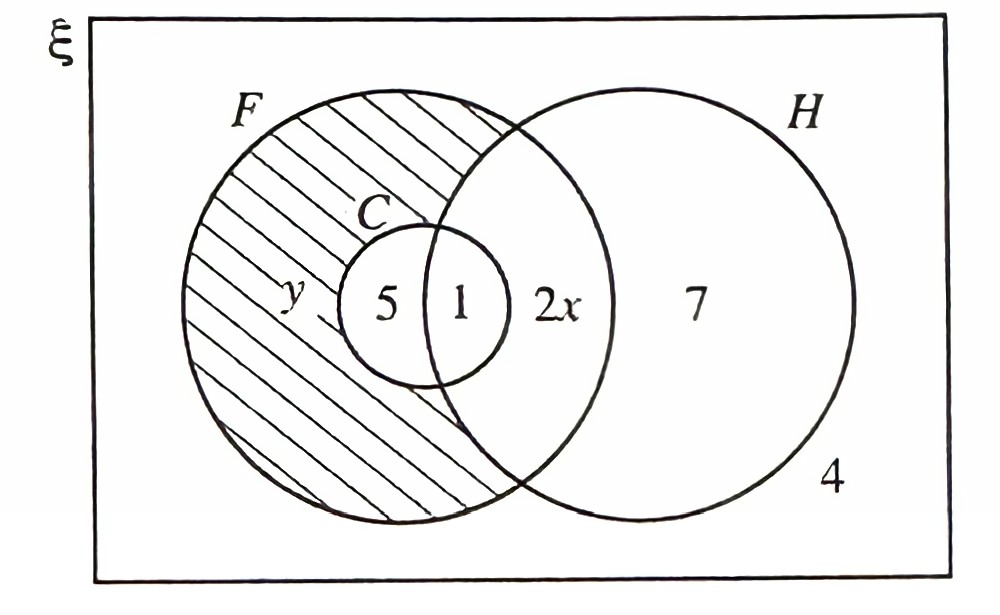
(i) The total number of students at the camp is 24 . There are 10 students who take part in at least two activities.
Calculate the value of x and the value of y.
[4 marks]
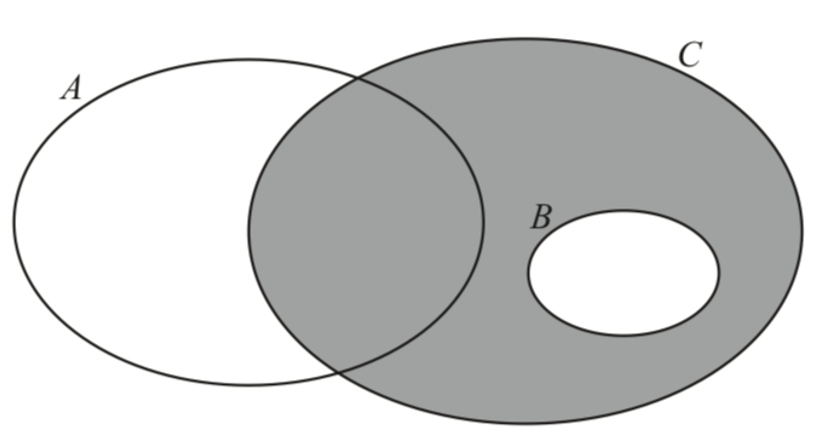
(ii) Represent the shaded region in Diagram 10.2 by using symbols ‘∪’ and/or ‘∩’.
[2 marks]
Answer:
(a)(i)(a)
{fishing, cooking}
(a)(i)(b)
{swimming, cycling}
(a)(ii)
(b)(i)
$$ \begin{aligned} 5+1+2 x & =10 \\ x & =2 \end{aligned} $$
$$ \begin{aligned} y+5+1+2(2)+7+4 & =24 \\ y & =3 \end{aligned} $$
(b)(ii)
$$ F \cap(C \cup H)^{\prime} $$
(a) Diagram 10.1 is a Venn diagram that shows the favourite activities of three students. It is given that
universal set, ξ = A ∪ B ∪ C,
set A = {Azmil’s favourite activities},
set B = {Beng’s favourite activity},
set C = {Canny’s favourite activities}.

(i) Using the set notation, list the activities that are
(a) Azmil’s favourite activities only,
(b) Canny’s favourite activities but not Beng’s favourite activity.
[2 marks]
(ii) On the diagram in the answer space, shade the set C ∩ B‘.
[1 mark]
Answer:
(a)(ii)

(b) The Venn diagram as shown in Diagram 10.2 represents the number of students taking part in activities at a camp. In the Venn diagram,
universal set, ξ = {all students at the camp},
set F = {students taking part in fishing},
set C = {students taking part in cooking},
set H = {students taking part in hiking}.

(i) The total number of students at the camp is 24 . There are 10 students who take part in at least two activities.
Calculate the value of x and the value of y.
[4 marks]
(ii) Represent the shaded region in Diagram 10.2 by using symbols ‘∪’ and/or ‘∩’.
[2 marks]
Answer:
(a)(i)(a)
{fishing, cooking}
(a)(i)(b)
{swimming, cycling}
(a)(ii)

(b)(i)
$$ \begin{aligned} 5+1+2 x & =10 \\ x & =2 \end{aligned} $$
$$ \begin{aligned} y+5+1+2(2)+7+4 & =24 \\ y & =3 \end{aligned} $$
(b)(ii)
$$ F \cap(C \cup H)^{\prime} $$