Question 9:
Diagram 6 shows graph OABCD and graph OPQRS. Graph OABCD represents the motion of particle X and graph OPQRS represents the motion of particle Y.
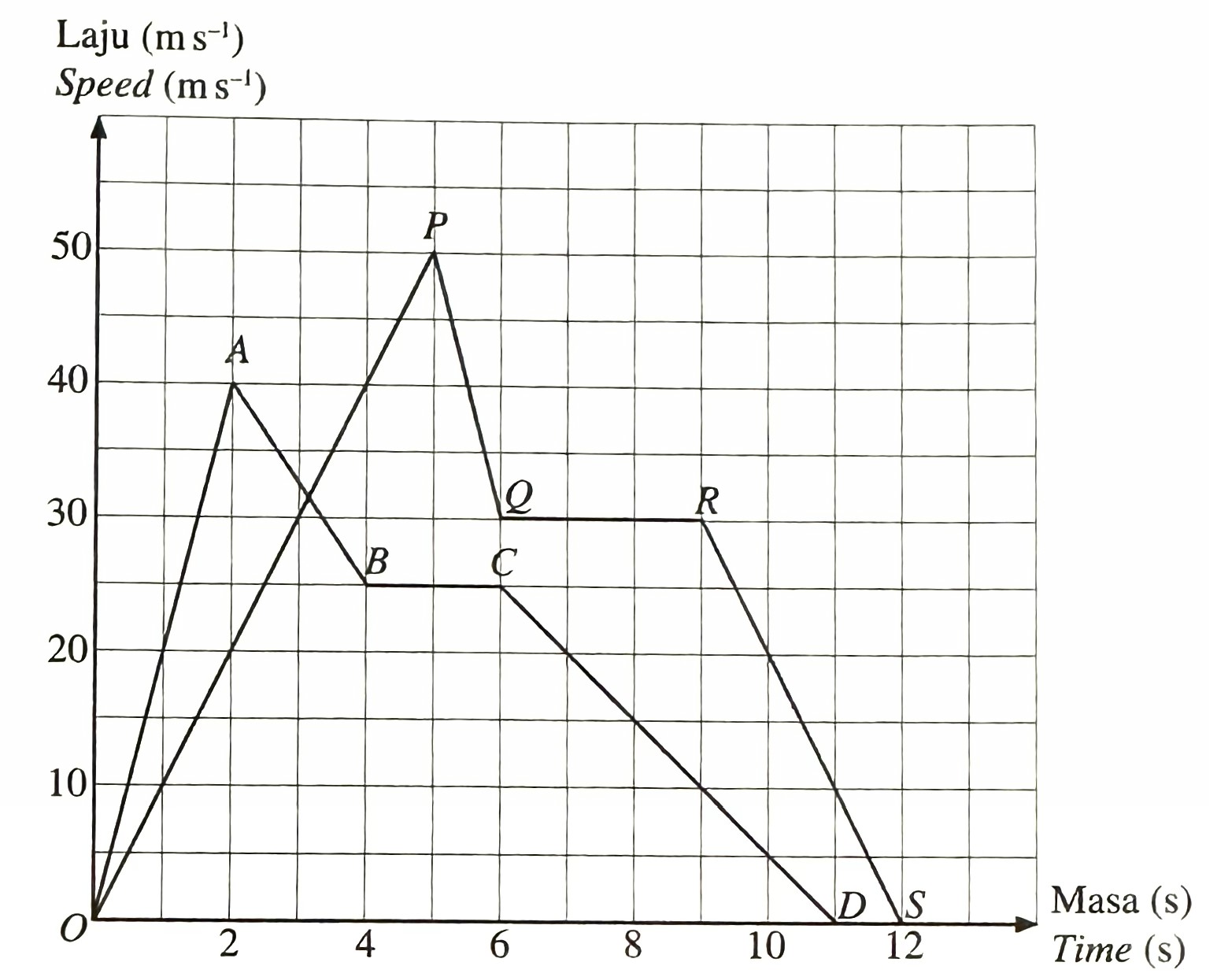
(a) State the uniform speed, in m s-1, of particle X.
[1 mark]
(b)(i) find the rate of change of speed, in m s-2, of particle Y for the first 5 seconds.
[1 mark]
(ii) calculate the difference between the distance, in m , travelled by particle X and particle Y after the 6th second until they stop.
[3 marks]
Answer:
(a) 25 m s-1
(b)(i)
$$ \begin{aligned} \text { Rate of change of speed } & =\frac{50 \mathrm{~m} \mathrm{~s}^{-1}}{5 \mathrm{~s}} \\ & =10 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
(b)(ii)
$$ \begin{aligned} &\text { The difference between distance }\\ &\begin{aligned} & =\left[\frac{1}{2}(3+6)(30)\right]-\left[\frac{1}{2}(5)(25)\right] \\ & =135 \mathrm{~m}-62.5 \mathrm{~m} \\ & =72.5 \mathrm{~m} \end{aligned} \end{aligned} $$
Diagram 6 shows graph OABCD and graph OPQRS. Graph OABCD represents the motion of particle X and graph OPQRS represents the motion of particle Y.

(a) State the uniform speed, in m s-1, of particle X.
[1 mark]
(b)(i) find the rate of change of speed, in m s-2, of particle Y for the first 5 seconds.
[1 mark]
(ii) calculate the difference between the distance, in m , travelled by particle X and particle Y after the 6th second until they stop.
[3 marks]
Answer:
(a) 25 m s-1
(b)(i)
$$ \begin{aligned} \text { Rate of change of speed } & =\frac{50 \mathrm{~m} \mathrm{~s}^{-1}}{5 \mathrm{~s}} \\ & =10 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
(b)(ii)
$$ \begin{aligned} &\text { The difference between distance }\\ &\begin{aligned} & =\left[\frac{1}{2}(3+6)(30)\right]-\left[\frac{1}{2}(5)(25)\right] \\ & =135 \mathrm{~m}-62.5 \mathrm{~m} \\ & =72.5 \mathrm{~m} \end{aligned} \end{aligned} $$
Question 10:
Azlan rode a Ferris wheel. Diagram 7 shows the graph of a trigonometric function representing the height of his seat on the Ferris wheel.
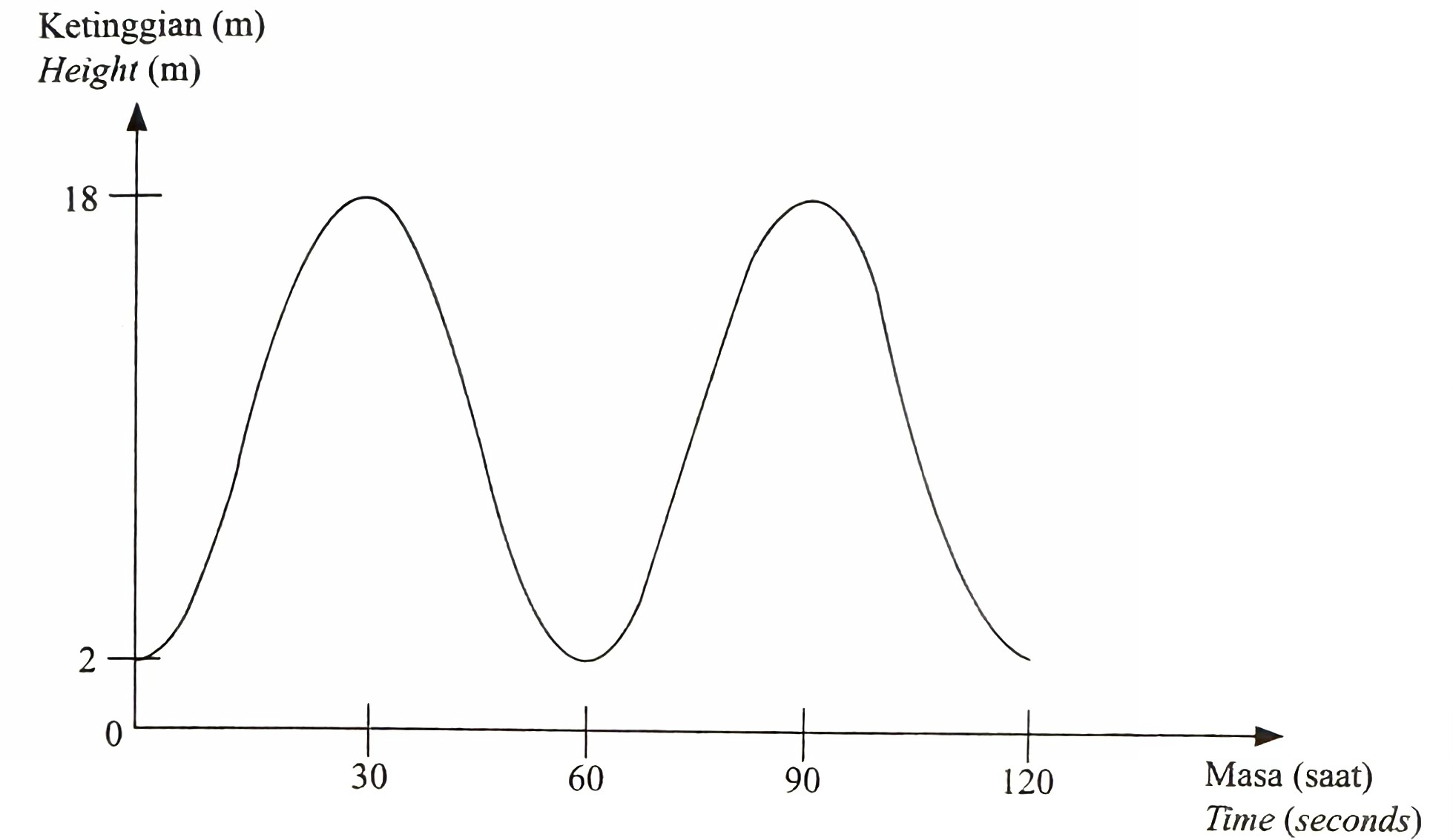
(a) It is given that y represents the height, in m , of the seat after x seconds. This situation can be modelled by the function, y = –a cos bx + 10.
State the value of a and the value of b.
[2 marks]
(b) Hence, determine the height, in m , of Azlan’s seat at the 73rd second.
[2 marks]
Answer:
(a)
$$ \begin{aligned} y & =-a \mathrm{cos} \ b x+10 \\ a & =\frac{18-2}{2} \\ & =8 \\ b & =\frac{360^{\circ}}{60} \\ & =6 \end{aligned} $$
(b)
$$ \begin{aligned} & y=-8 \mathrm{cos} \ 6 x+10 \\ & y=-8 \mathrm{cos} \ 6(73)+10 \\ & y=-8 \mathrm{cos} \ (438)+10 \\ & y=8.34 \mathrm{~m} \end{aligned} $$
Azlan rode a Ferris wheel. Diagram 7 shows the graph of a trigonometric function representing the height of his seat on the Ferris wheel.

(a) It is given that y represents the height, in m , of the seat after x seconds. This situation can be modelled by the function, y = –a cos bx + 10.
State the value of a and the value of b.
[2 marks]
(b) Hence, determine the height, in m , of Azlan’s seat at the 73rd second.
[2 marks]
Answer:
(a)
$$ \begin{aligned} y & =-a \mathrm{cos} \ b x+10 \\ a & =\frac{18-2}{2} \\ & =8 \\ b & =\frac{360^{\circ}}{60} \\ & =6 \end{aligned} $$
(b)
$$ \begin{aligned} & y=-8 \mathrm{cos} \ 6 x+10 \\ & y=-8 \mathrm{cos} \ 6(73)+10 \\ & y=-8 \mathrm{cos} \ (438)+10 \\ & y=8.34 \mathrm{~m} \end{aligned} $$