Question 9:
Table 1 shows the name of four boys and a girl in SMK Pelangi who are assigned to raise the flag during the school assembly.
 Table 1
Table 1
Two pupils are chosen at random to raise the flag.
(a) List all the possible outcomes of the event for this sample space.
You may use the capital letter such as A for Adam and so on. [2 marks]
(b) By listing down all the possible outcomes of the event, find the probability that
(i) the students chosen are of different gender,
(ii) Borhan and Daljit are not assigned together. [4 marks]
Solution:
(a)
A = Adam, B = Borhan, C = Chan, D = Daljit, E = Elina
S = {AB, AC, AD, AE, BC, BD, BE, CD, CE, DE}
(b)(i)
{AE, BE, CE, DE}
(b)(ii)
{BD}
Table 1 shows the name of four boys and a girl in SMK Pelangi who are assigned to raise the flag during the school assembly.
 Table 1
Table 1Two pupils are chosen at random to raise the flag.
(a) List all the possible outcomes of the event for this sample space.
You may use the capital letter such as A for Adam and so on. [2 marks]
(b) By listing down all the possible outcomes of the event, find the probability that
(i) the students chosen are of different gender,
(ii) Borhan and Daljit are not assigned together. [4 marks]
Solution:
(a)
A = Adam, B = Borhan, C = Chan, D = Daljit, E = Elina
S = {AB, AC, AD, AE, BC, BD, BE, CD, CE, DE}
(b)(i)
{AE, BE, CE, DE}
(b)(ii)
{BD}
Question 10:
Diagram 5 shows an oil tanker. The oil tank of the lorry is a cylindrical with 20 m length and 2.1 m in radius. The tank is half filled with oil.
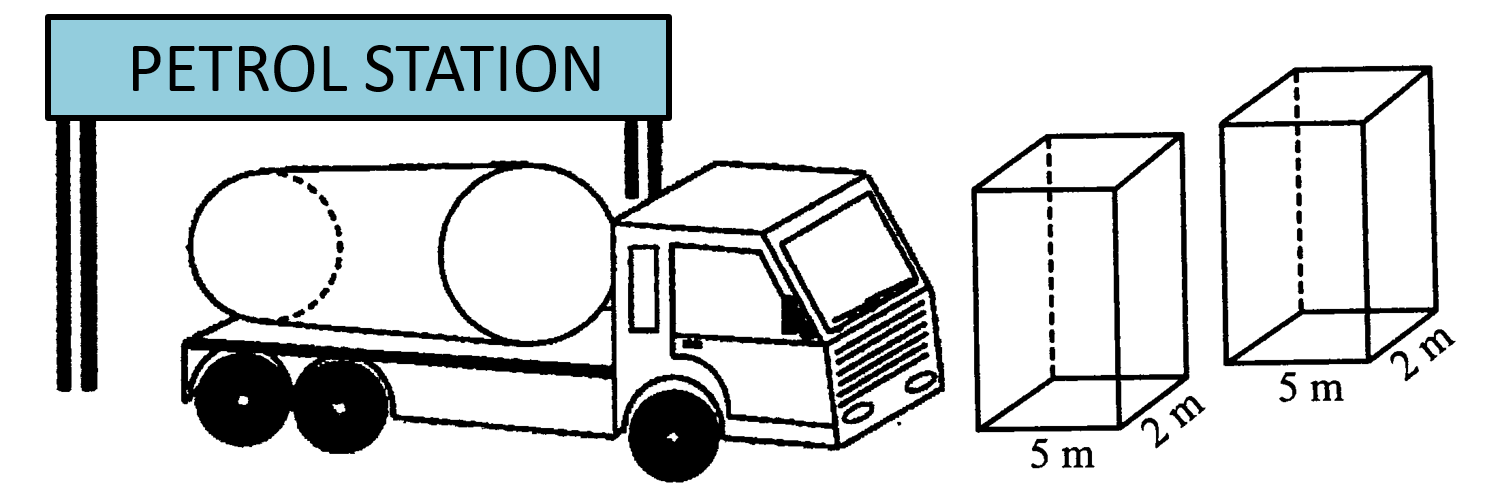 Diagram 5
Diagram 5
Upon arrival at a petrol station, all of the fuel in the tanker was pumped out equally into 2 cuboidal tanks, built underground.
Using , calculate the height, in m, of the oil level in the tank. [4 marks]
Solution:
Diagram 5 shows an oil tanker. The oil tank of the lorry is a cylindrical with 20 m length and 2.1 m in radius. The tank is half filled with oil.
 Diagram 5
Diagram 5Upon arrival at a petrol station, all of the fuel in the tanker was pumped out equally into 2 cuboidal tanks, built underground.
Using , calculate the height, in m, of the oil level in the tank. [4 marks]
Solution: