(E) Converting from One Base to Another
1. The following steps are used to convert a number from one base to another base.
(a) convert the number to a number in base 10 by using expended notation.
(b) use repeated division to convert the number in base 10 to the respective bases.
Example 1:
Convert
(a) 1101012 to a number in base 5
(b) 435 to a number in base 2
(c) 3138 to a number in base 5
(d) 4225 to a number in base 8
(e) 1001112 to a number in base 8
(f) 1578 to a number in base 2
(f) 1578 to a number in base 2
Solution:
(a) 1101012
= 1 × 25 + 1 × 24 + 0 × 23+ 1 × 22 + 0 × 21 + 1 × 20
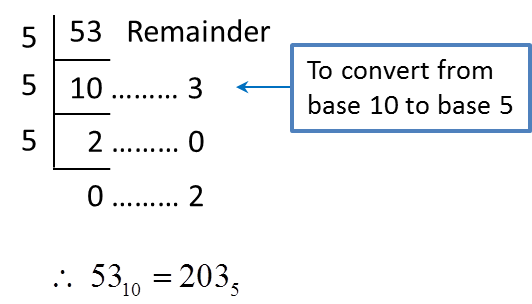
= 5310 ← (Convert from base 2 to base 10)
(b) 435
= 4 × 51 + 3 × 50
= 2310← (Convert from base 5 to base 10)
(c) 3138
= 3 × 82 + 1 × 81 + 3 × 80
= 20310← (Convert from base 8 to base 10)
(d) 4225
= 4 × 52 + 2 × 51 + 2 × 50
= 11210← (Convert from base 5 to base 10)
(e) 1001112
= 1 × 25 + 0 × 24 + 0 × 23+ 1 × 22 + 1 × 21 + 1 × 20
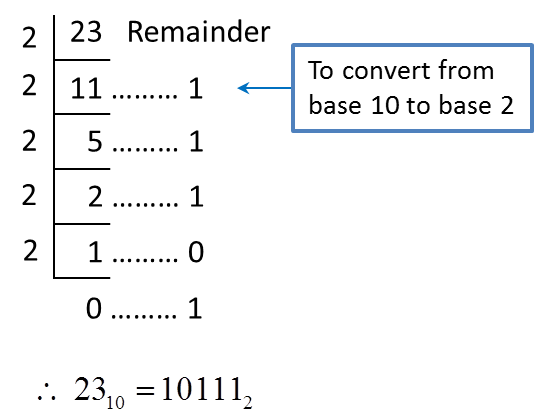
= 3910 ← (Convert from base 2 to base 10)

(f) 1578
= 1 × 82 + 5 × 81 + 7 × 80
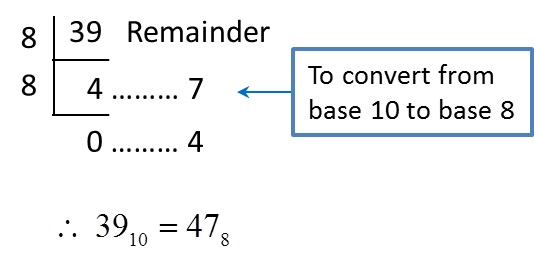
= 11110← (Convert from base 8 to base 10)

Calculator Computation
1. Set the calculator to the ‘BASE’ mode by pressing:
[MODE] [MODE] [3 (BASE)]
2. Set the calculator to the desired number system by pressing:
[BIN] → for base 2
[DEC] → for base 10
[OCT] → for base 8
Key in the following [For (e) and (f) only]:
(e)
[ BIN ] 100111 [ = ] [ OCT ]
The screen display is: [478]
Therefore 1001112 = 478
(f)
[ OCT ] 157 [ = ] [ BIN ]
The screen display is: [1101111]
Therefore 1578 = 11011112
|



How to express 8^5 as a number base 8 ?
isnt (d) 111 when converted to base 10, if im wrong pls correct me
rsvp