Question 5 (4 marks):
Diagram 5 shows a cylindrical tank in a residential area which have 125 houses. Each house received equal volume of water.
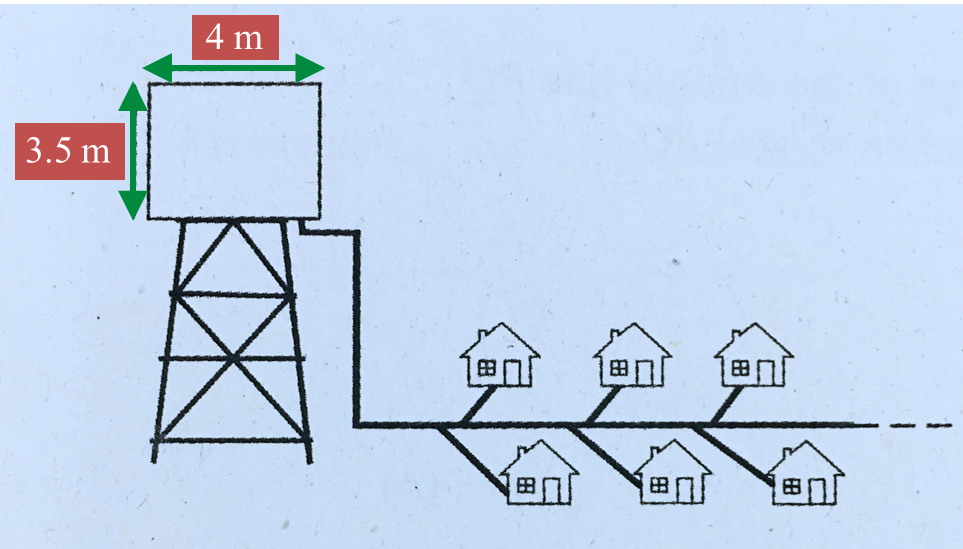 Diagram 5
Diagram 5
The diameter of the cylindrical tank is 4 m. It is given that each house has a cuboid tank with a base area of 0.8 m2.
Using , calculate the height of the water level, in m, of each tank in the house.
Solution:
Diagram 5 shows a cylindrical tank in a residential area which have 125 houses. Each house received equal volume of water.
 Diagram 5
Diagram 5The diameter of the cylindrical tank is 4 m. It is given that each house has a cuboid tank with a base area of 0.8 m2.
Using , calculate the height of the water level, in m, of each tank in the house.
Solution:
Question 6 (5 marks):
Diagram 6 shows two parallel straight lines, POQ and RMS drawn on a Cartesian plane.
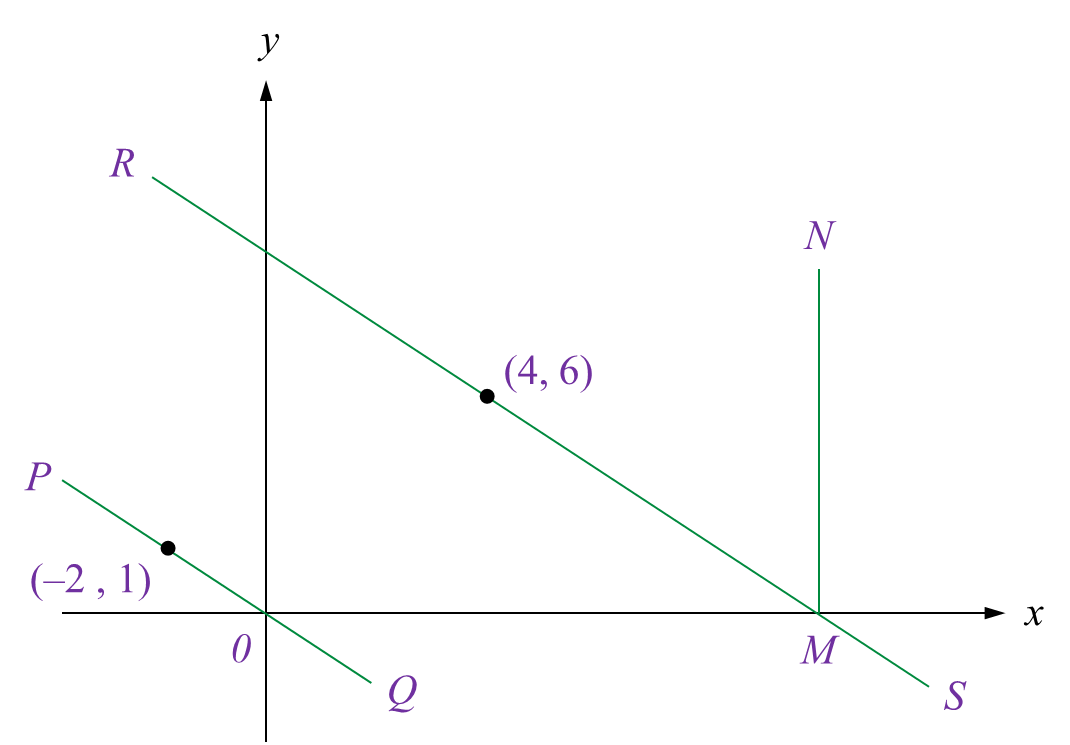 Diagram 6
Diagram 6
Find
(a) the equation of the straight line RMS,
(b) the x-intercept of the straight line MN.
Solution:
(a)
(b)
Diagram 6 shows two parallel straight lines, POQ and RMS drawn on a Cartesian plane.
 Diagram 6
Diagram 6Find
(a) the equation of the straight line RMS,
(b) the x-intercept of the straight line MN.
Solution:
(a)
(b)