9.5.2 Probability (II), SPM Practice (Long Questions)
Question 3:
Diagram below shows two cards labelled with letters in box A and three numbered cards in box B.
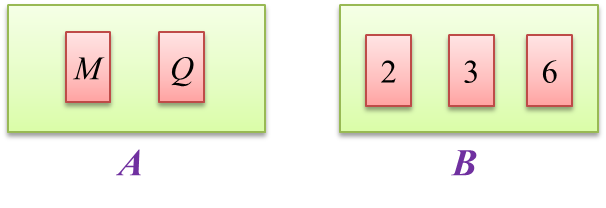

A card is picked at random from box A and then a card is picked at random from box B.
By listing the sample of all possible outcomes of the event, find the probability that
(a) a card labelled M and a card with an even number are picked,
(b) a card labelled Q or a card with a number which is multiple of 2 are picked.
Solution:
Sample space, S
= {(M, 2), (M, 3), (M, 6), (Q, 2), (Q, 3), (Q, 6)}
n(S) = 6
(a)
{(M, 2), (M, 6)}
(b)
{(Q, 2), (Q, 3), (Q, 6), (M, 2), (M, 6)}Question 4:
Table below shows the names of participants from two secondary schools attending a public speaking training programme.
Boys |
Girls |
|
School A |
Karim |
Rosita
Sally
Linda |
School B |
Ahmad
Billy |
Nancy |
Two participants are required to give speeches at the end of the programme.
(a) A participant is chosen at random from School A and then another participant is chosen at random also from School A.
(i) List all the possible outcomes of the event in this sample space.
(ii)Hence, find the probability that a boy and a girl are chosen.
(b) A participant is chosen at random from the boys group and then another participant is chosen at random from the girls group.
(i) List all the possible outcomes of the event in this sample space.
(ii)Hence, find the probability that both participants chosen are from School B.
Solution:
(a)(i)
Sample space, S
= {(Karim, Rosita), (Karim, Sally), (Karim, Linda), (Rosita, Sally), (Rosita, Linda), (Sally, Linda)}
n(S) = 6
(a)(ii)
{(Karim, Rosita), (Karim, Sally), (Karim, Linda}
(b)(i)
Sample space, S
= {(Karim, Rosita), (Karim, Sally), (Karim, Linda), (Karim, Nancy), (Ahmad, Rosita), (Ahmad, Sally), (Ahmad, Linda), (Ahmad, Nancy), (Billy, Rosita), (Billy, Sally), (Billy, Linda), (Billy, Nancy)}
n(S) = 12
(b)(ii)
{(Ahmad, Nancy), (Billy, Nancy)}
P (both participants from School B)

