Question 7:
(c) From your graph, find
(d) Draw a suitable straight line on your graph to find the values of x which satisfy the equation –x3 + 13x – 9 = 0 for –3 ≤ x ≤ 4 and –51 ≤ y ≤ 19.
Solution:
(d)
(a) The following table shows the corresponding values of x and y for the
equation y= –x3 + 3x + 1.
equation y= –x3 + 3x + 1.
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
3.5 |
4 |
y |
19 |
3 |
r |
1 |
3 |
–1 |
s |
–31.4 |
–51 |
Calculate the value of r and s.
(b) For this part of the question, use graph paper. You may use a flexible curve rule.
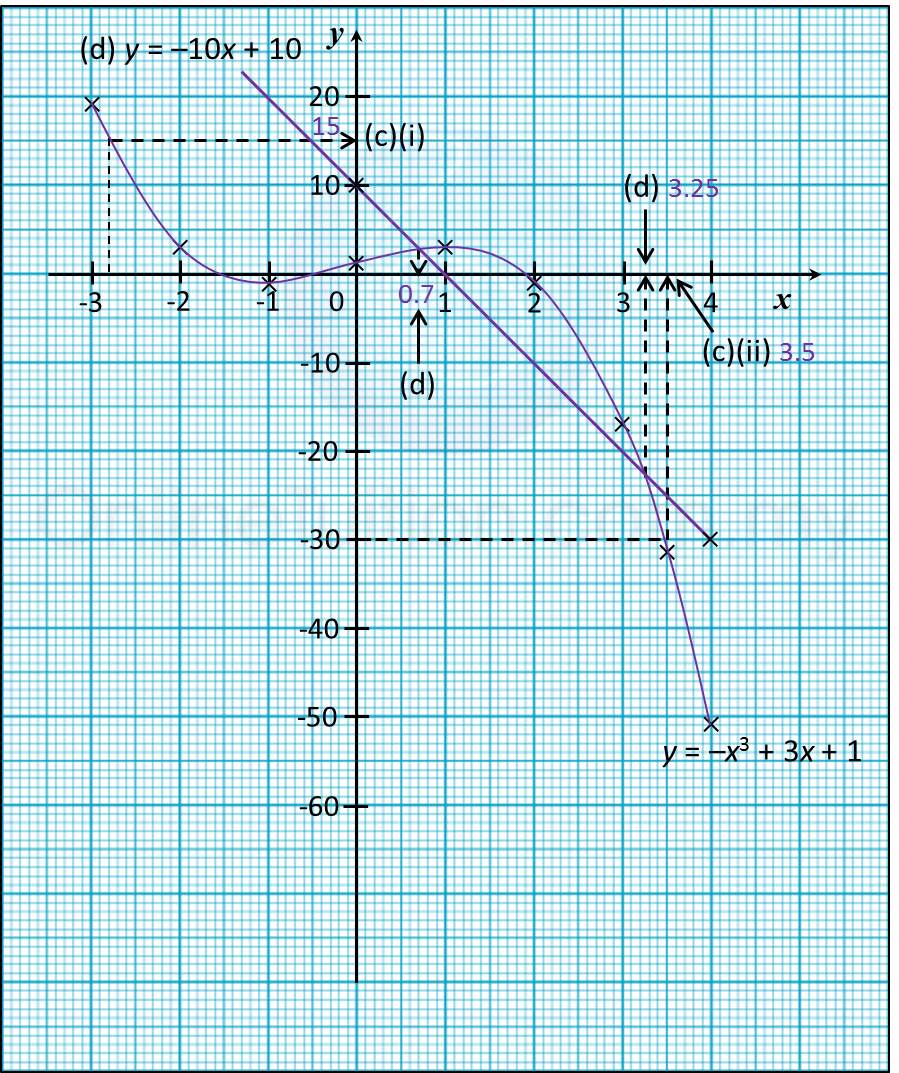
By using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the y-axis, draw the graph of y = –x3 + 3x + 1 for –3 ≤ x ≤ 4 and –51 ≤ y ≤ 19.
(c) From your graph, find
(i) The value of y when x = –2.8,
(ii) The value of x when y = –30.
(d) Draw a suitable straight line on your graph to find the values of x which satisfy the equation –x3 + 13x – 9 = 0 for –3 ≤ x ≤ 4 and –51 ≤ y ≤ 19.
(a)
y= –x3 + 3x + 1
when x = –1,
r = – (–1)3 + 3(–1) + 1
= 1 – 3 + 1 = –1
when x = 3,
s = – (3)3 + 3(3) + 1 = –17
(b)

(c)
(i) From the graph, when x = –2.8, y = 15
(ii) From the graph, when y = –30, x = 3.5
(d)
y = –x3 + 3x+ 1 —– (1)
–x3+ 13x – 9 = 0 —– (2)
y = –x3 + 3x + 1 —– (1)
0 = –x3 + 13x – 9 —— (2) ← (Rearrange (2))
(1) – (2) : y = –10x + 10
The suitable straight line is y = –10x + 10.
Determine the x-coordinates of the two points of intersection of the curve
y = –x3 + 3x + 1 and the straight line y = –10x + 10.
x |
0 |
4 |
y = –10x + 10 |
10 |
–30 |
From the graph, x= 0.7, 3.25.
Question 8:
(a) Complete the table in the answer space for the equation y = x3 – 4x – 10 by writing down the values of y when x = –1 and x = 3.
(b) For this part of the question, use graph paper. You may use a flexible curve rule.
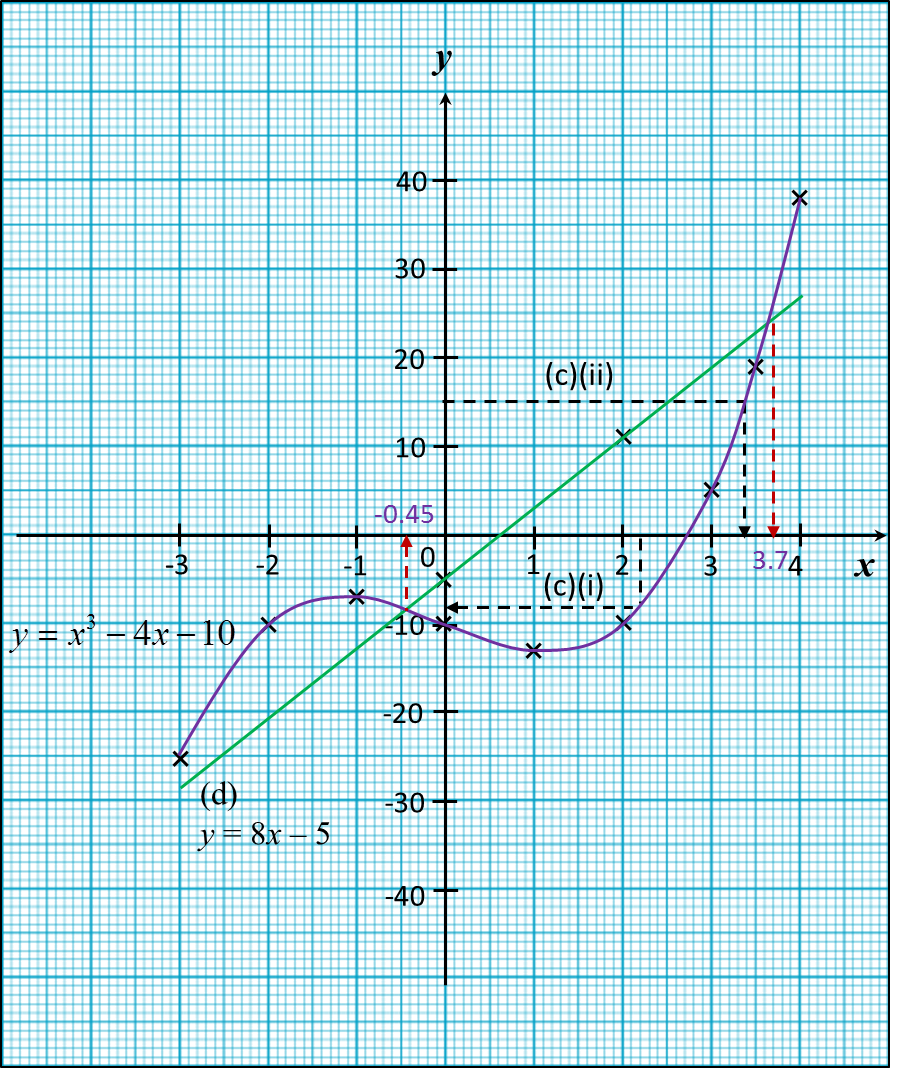
By using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 10 units on the y-axis, draw the graph of y = x3 – 4x – 10 for –3 ≤ x ≤ 4 and –25 ≤ y ≤ 38.
(c) From your graph, find
(i) the value of y when x = 2.2,
(ii) the value of x when y = 15.
(d) Draw a suitable straight line on your graph to find the values of x which satisfy the equation x3 – 12x – 5 = 0 for –3 ≤ x ≤ 4 and –25 ≤ y ≤ 38.
Answer:
Solution:
(a)
y = x3 – 4x – 10
when x = –1,
y = (–1)3 – 4(–1) – 10
= –7
when x = 3,
y = (3)3 – 4(3) – 10
= 5
(b)
(c)
(i) From the graph, when x = 2.2, y = –8
(ii) From the graph, when y = 15, x = 3.4
(d)
y = x3 – 4x – 10 ----- (1)
0 = x3 – 12x – 5 ----- (2)
(1) – (2) : y = 8x – 5
The suitable straight line is y = 8x–5. Determine the x-coordinates of the two points of intersection of the curve y = x3 – 4x – 10 and the straight line y = 8x –5.
From the graph, x = –0.45, 3.7.
(a) Complete the table in the answer space for the equation y = x3 – 4x – 10 by writing down the values of y when x = –1 and x = 3.
(b) For this part of the question, use graph paper. You may use a flexible curve rule.
By using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 10 units on the y-axis, draw the graph of y = x3 – 4x – 10 for –3 ≤ x ≤ 4 and –25 ≤ y ≤ 38.
(c) From your graph, find
(i) the value of y when x = 2.2,
(ii) the value of x when y = 15.
(d) Draw a suitable straight line on your graph to find the values of x which satisfy the equation x3 – 12x – 5 = 0 for –3 ≤ x ≤ 4 and –25 ≤ y ≤ 38.
Answer:
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
3.5 |
4 |
y |
–25 |
–10 |
–10 |
–13 |
–10 |
18.9 |
38 |
Solution:
(a)
y = x3 – 4x – 10
when x = –1,
y = (–1)3 – 4(–1) – 10
= –7
when x = 3,
y = (3)3 – 4(3) – 10
= 5
(b)

(c)
(i) From the graph, when x = 2.2, y = –8
(ii) From the graph, when y = 15, x = 3.4
(d)
y = x3 – 4x – 10 ----- (1)
0 = x3 – 12x – 5 ----- (2)
(1) – (2) : y = 8x – 5
The suitable straight line is y = 8x–5. Determine the x-coordinates of the two points of intersection of the curve y = x3 – 4x – 10 and the straight line y = 8x –5.
x |
0 |
2 |
y = 8x – 5 |
–5 |
–11
|