Question 4:
Solution:

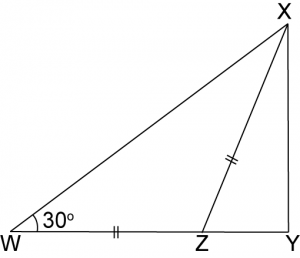
In the diagram above, WZY is a straight line.
and WZ = XZ = 30 cm. Find the length of XY.
Solution:
Question 5:
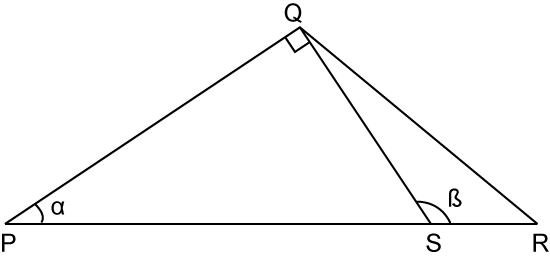
In the diagram above, PQS is a right angle triangle. Given that SR = 6cm, PQ = 12 cm and 5SR = 2PS. Find the value of cos α and tan β.
Solution:

In the diagram above, PQS is a right angle triangle. Given that SR = 6cm, PQ = 12 cm and 5SR = 2PS. Find the value of cos α and tan β.
Solution:
Question 6:
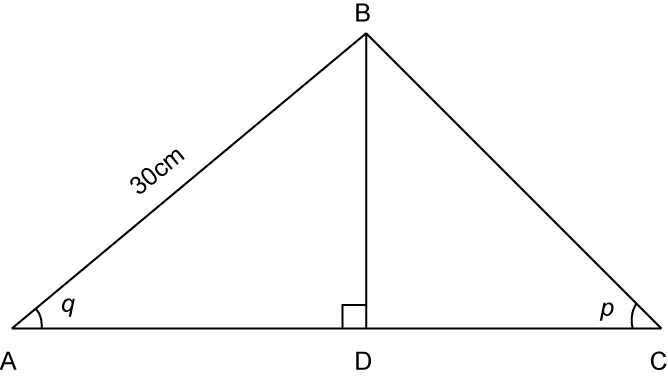
In the diagram above, ADC is a straight line, if . Find the distance of AC.
Solution:

In the diagram above, ADC is a straight line, if . Find the distance of AC.
Solution:
Hi, for question 5 the answer for cos alpha is 4/5 not 3/5. Please correct the simplification.
Dear Gurdit Singh,
thanks for pointing out our mistake, correction had been made accordingly.
question 5 cos alpha should be 4/5 and not 3/5 as 12/15(which is correct) equals to 4/5
Dear donald,
thanks for pointing out our mistake, correction had been made accordingly.