Question 3:
(b) Based on the completed table above,
Solution:
(a)
(b)(i)
(b)(ii)
(c)
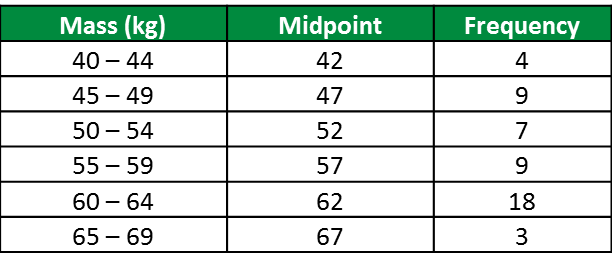
The data below shows the mass, in kg, of 50 students.
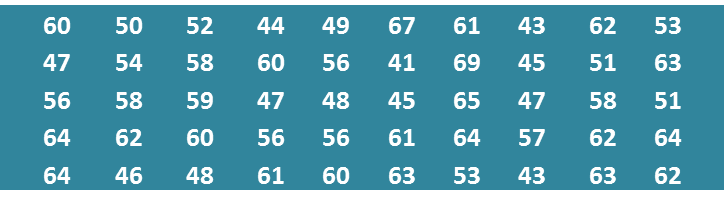
(a) Copy and complete the table below based on the data above.
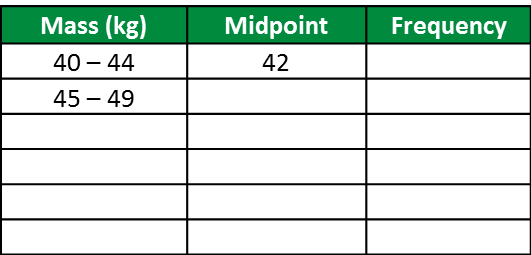

(a) Copy and complete the table below based on the data above.

(b) Based on the completed table above,
(i) State the size of the class interval used in the table.
(ii) Calculate the estimated mean of the mass of the students.
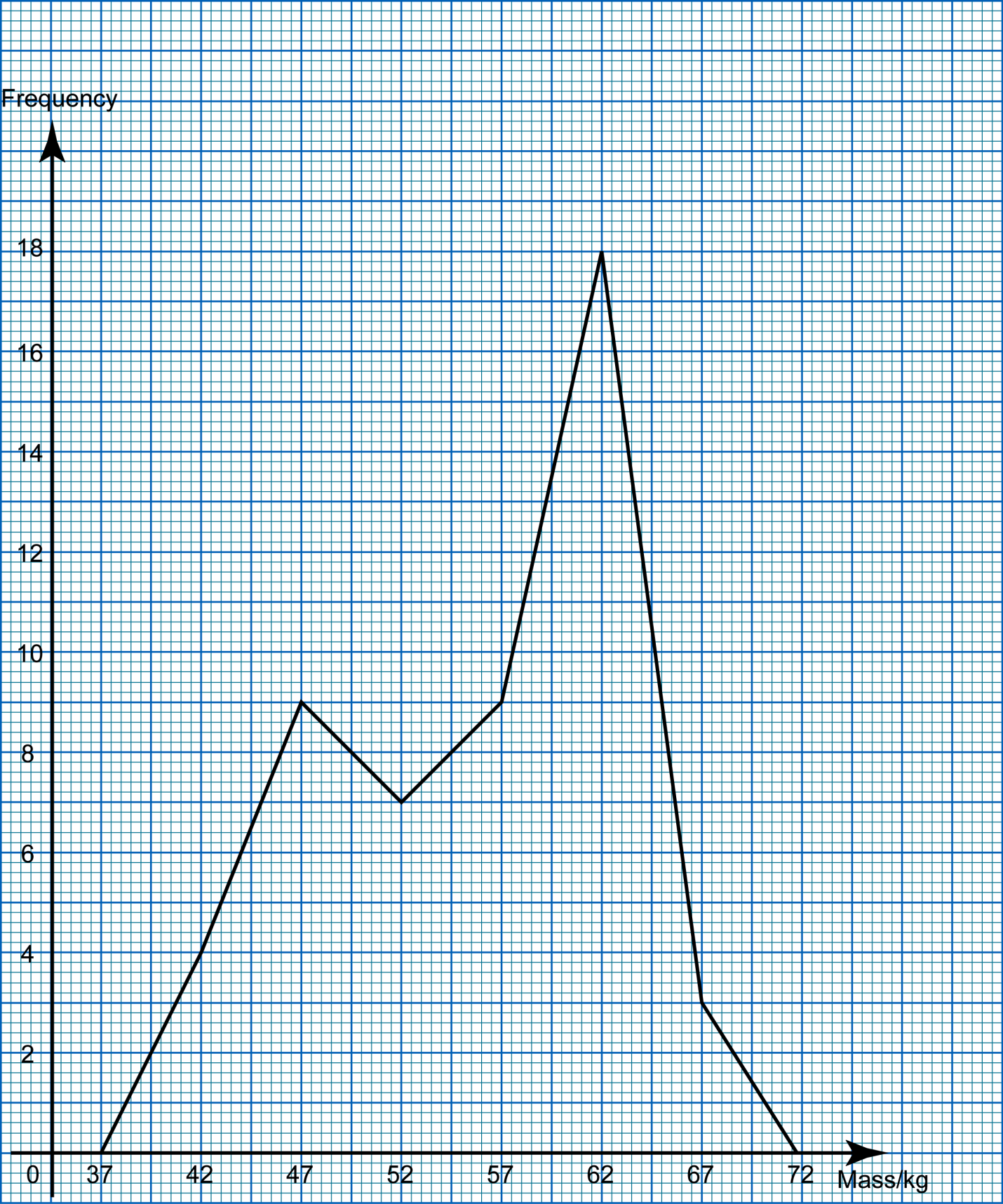
For this part of the question, use graph paper.
(c) By using a scale of 2 cm to 5 kg on the horizontal axis and 2 cm to 2 students on the vertical axis, draw a frequency polygon for the data.
For this part of the question, use graph paper.
(c) By using a scale of 2 cm to 5 kg on the horizontal axis and 2 cm to 2 students on the vertical axis, draw a frequency polygon for the data.
(a)

(b)(i)
Size of class interval
= upper boundary – lower boundary
= 44.5 – 39.5
= 5
(b)(ii)
(c)

Question 4:
Diagram below shows the marks obtained by a group of 30 students in a Science test.
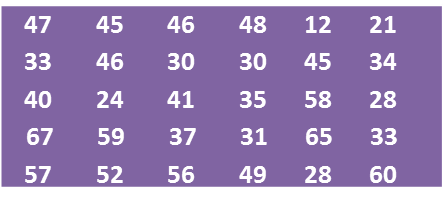
(a) Based on the data in diagram above, complete the table in the answer space.
(b) Based on the completed table in part (a), calculate the estimated mean mark of a student.
For this part of the question, use graph paper.
(c) By using a scale of 2 cm to 10 marks on the horizontal axis and 2 cm to 1 student on the vertical axis, draw a frequency polygon for the data.
(d) The passing mark for the test is 44. Using the frequency polygon drawn in part (c), find the number of students who passed the test.
Answer:
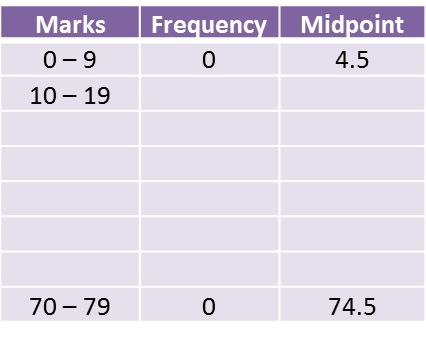
Solution:
(a)
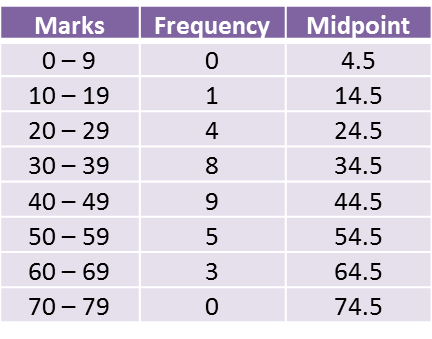
(b)
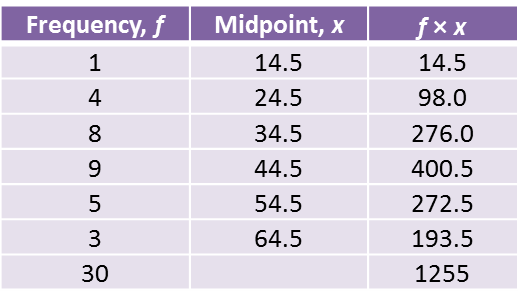
(c)
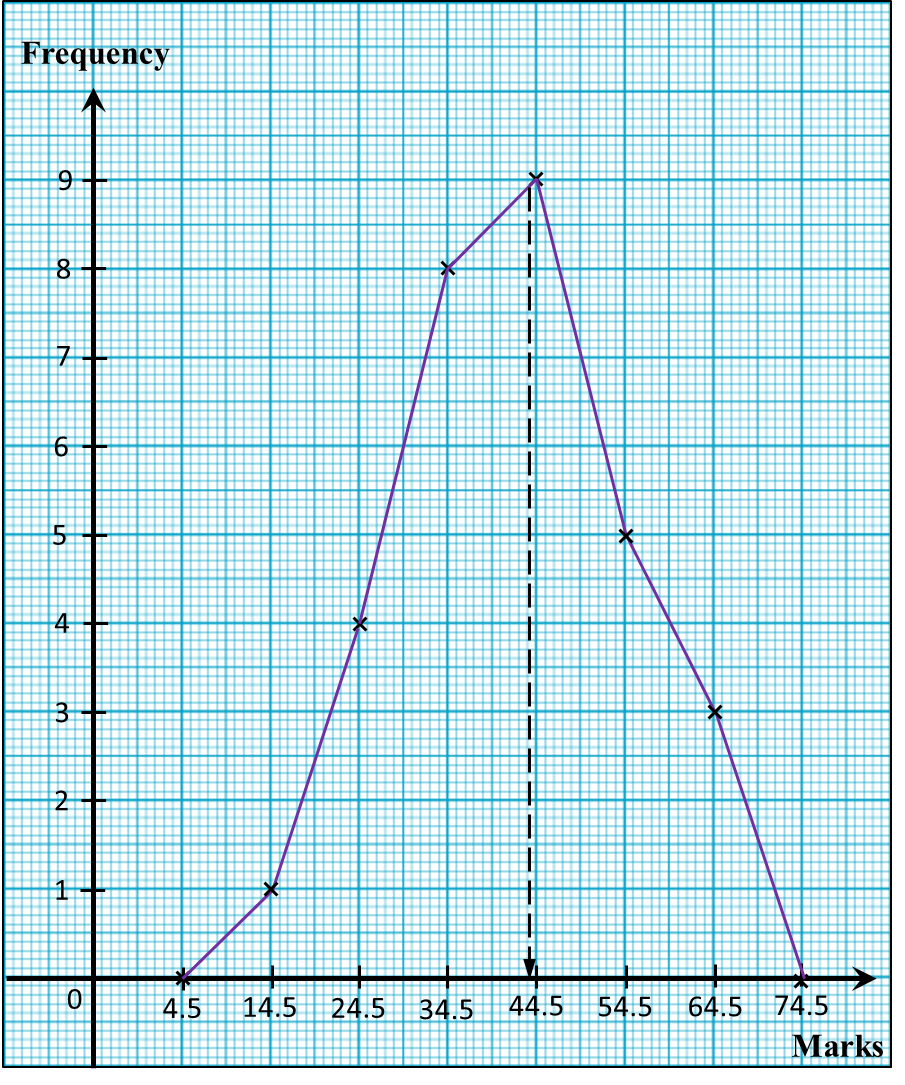
(d)
Number of students who passed the test
= 9 + 5 + 3
= 17
Diagram below shows the marks obtained by a group of 30 students in a Science test.

(a) Based on the data in diagram above, complete the table in the answer space.
(b) Based on the completed table in part (a), calculate the estimated mean mark of a student.
For this part of the question, use graph paper.
(c) By using a scale of 2 cm to 10 marks on the horizontal axis and 2 cm to 1 student on the vertical axis, draw a frequency polygon for the data.
(d) The passing mark for the test is 44. Using the frequency polygon drawn in part (c), find the number of students who passed the test.
Answer:

Solution:
(a)

(b)

(c)

(d)
Number of students who passed the test
= 9 + 5 + 3
= 17